IB DP Maths: AA SL复习笔记3.6.4 Linear Trigonometric Equations
Trigonometric Equations: sinx = k
How are trigonometric equations solved?
- Trigonometric equations can have an infinite number of solutions
- For an equation in sin or cos you can add 360° or 2π to each solution to find more solutions
- For an equation in tan you can add 180° or π to each solution
- When solving a trigonometric equation you will be given a range of values within which you should find all the values
- Solving the equation normally and using the inverse function on your calculator or your knowledge of exact values will give you the primary value
- The secondary values can be found with the help of:
- The unit circle
- The graphs of trigonometric functions
How are trigonometric equations of the form sin x = k solved?
- It is a good idea to sketch the graph of the trigonometric function first
- Use the given range of values as the domain for your graph
- The intersections of the graph of the function and the line y = k will show you
- The location of the solutions
- The number of solutions
- You will be able to use the symmetry properties of the graph to find all secondary values within the given range of values
- The method for finding secondary values are:
- For the equation sin x = k the primary value is x1 = sin -1 k
- A secondary value is x2 = 180° - sin -1 k
- Then all values within the range can be found using x1 ± 360n and
- For the equation sin x = k the primary value is x1 = sin -1 k
Exam Tip
- If you are using your GDC it will only give you the principal value and you need to find all other solutions for the given interval
- Sketch out the CAST diagram and the trig graphs on your exam paper to refer back to as many times as you need to
Worked Example
Trigonometric Equations: sin(ax + b) = k
How can I solve equations with transformations of trig functions?
- Trigonometric equations in the form sin(ax + b) can be solved in more than one way
- The easiest method is to consider the transformation of the angle as a substitution
- For example let u = ax + b
- Transform the given interval for the solutions in the same way as the angle
- For example if the given interval is 0° ≤ x ≤ 360° the new interval will be
- (a (0°) + b) ≤ u ≤ (a (360°) + b)
- Solve the function to find the primary value for u
- Use either the unit circle or sketch the graph to find all the other solutions in the range for u
- Undo the substitution to convert all of the solutions back into the corresponding solutions for x
- Another method would be to sketch the transformation of the function
- If you use this method then you will not need to use a substitution for the range of values
Exam Tip
- If you transform the interval, remember to convert the found angles back to the final values at the end!
- If you are using your GDC it will only give you the principal value and you need to find all other solutions for the given interval
- Sketch out the CAST diagram and the trig graphs on your exam paper to refer back to as many times as you need to
Worked Example
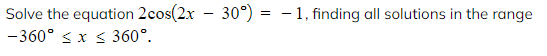
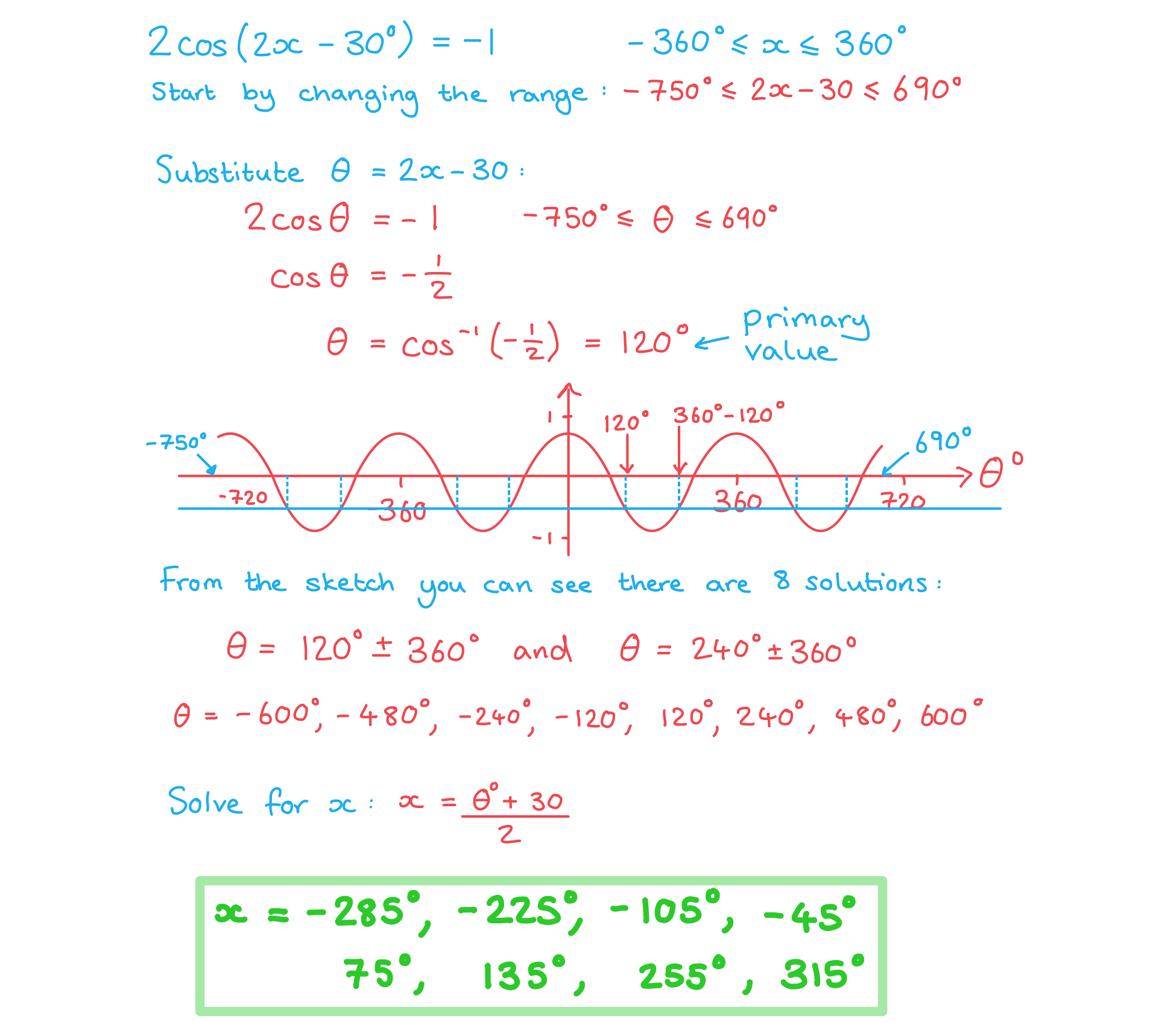
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
2025欧几里得数学竞赛报名开启！
