Home » 国际竞赛 » 数学国际竞赛 » AMC美国数学竞赛 » Details

【全网首发】2021AIME I 真题及答案

Category: AMC美国数学竞赛, 国际竞赛 Date: 2021年3月15日上午10:42

【全网首发】2021AIME I 真题及答案

文末答案

Problem1

Zou and Chou are practicing their 100-meter sprints by running $6$ races against each other. Zou wins the first race, and after that, the probability that one of them wins a race is $\frac23$ if they won the previous race but only $\frac13$ if they lost the previous race. The probability that Zou will win exactly $5$ of the $6$ races is $\frac mn$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Problem2

In the diagram below, $ABCD$ is a rectangle with side lengths $AB=3$ and $BC=11$ , and $AECF$ is a rectangle with side lengths $AF=7$ and $FC=9,$ as shown. The area of the shaded region common to the interiors of both rectangles is $\frac mn$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ . $[asy] pair A, B, C, D, E, F; A=(0,3); B=(0,0); C=(11,0); D=(11,3); E=foot(C, A, (9/4,0)); F=foot(A, C, (35/4,3)); draw(A--B--C--D--cycle); draw(A--E--C--F--cycle); filldraw(A--(9/4,0)--C--(35/4,3)--cycle,gray*0.5+0.5*lightgray); dot(A^^B^^C^^D^^E^^F); label("$A$", A, W); label("$B$", B, W); label("$C$", C, (1,0)); label("$D$", D, (1,0)); label("$F$", F, N); label("$E$", E, S); [/asy]$

Problem3

Find the number of positive integers less than $1000$ that can be expressed as the difference of two integral powers of $2.$

Problem4

Find the number of ways $66$ identical coins can be separated into three nonempty piles so that there are fewer coins in the first pile than in the second pile and fewer coins in the second pile than in the third pile.

Problem5

Call a three-term strictly increasing arithmetic sequence of integers special if the sum of the squares of the three terms equals the product of the middle term and the square of the common difference. Find the sum of the third terms of all special sequences.

Problem6

Segments $\overline{AB}, \overline{AC},$ and $\overline{AD}$ are edges of a cube and $\overline{AG}$ is a diagonal through the center of the cube. Point $P$ satisfies $PB=60\sqrt{10}, PC=60\sqrt{5}, PD=120\sqrt{2},$ and $PG=36\sqrt{7}$ . What is $PA$ ?

Problem7

Find the number of pairs $(m,n)$ of positive integers with $1\le m<n\le 30$ such that there exists a real number $x$ satisfying $\sin(mx)+\sin(nx)=2.$

Problem8

Find the number of integers $c$ such that the equation $\left||20|x|-x^2|-c\right|=21$ has $12$ distinct real solutions.

Problem 9

Let $ABCD$ be an isosceles trapezoid with $AD=BC$ and $AB<CD.$ Suppose that the distances from $A$ to the lines $BC,CD,$ and $BD$ are $15,18,$ and $10,$ respectively. Let $K$ be the area of $ABCD.$ Find $\sqrt2 \cdot K.$

Diagram

Problem 10

Consider the sequence $(a_k)_{k\ge 1}$ of positive rational numbers defined by $a_1 = \frac{2020}{2021}$ and for $k\ge 1$ , if $a_k = \frac{m}{n}$ for relatively prime positive integers $m$ and $n$ , then $a_{k+1} = \frac{m + 18}{n+19}.$ Determine the sum of all positive integers $j$ such that the rational number $a_j$ can be written in the form $\frac{t}{t+1}$ for some positive integer $t$ .

Problem 11

Let $ABCD$ be a cyclic quadrilateral with $AB=4,BC=5,CD=6,$ and $DA=7$ . Let $A_1$ and $C_1$ be the feet of the perpendiculars from $A$ and $C$ , respectively, to line $BD,$ and let $B_1$ and $D_1$ be the feet of the perpendiculars from $B$ and $D,$ respectively, to line $AC$ . The perimeter of $A_1B_1C_1D_1$ is $\frac mn$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .

Diagram

Problem 12

Let $A_1A_2A_3...A_{12}$ be a dodecagon (12-gon). Three frogs initially sit at $A_4,A_8,$ and $A_{12}$ . At the end of each minute, simultaneously, each of the three frogs jumps to one of the two vertices adjacent to its current position, chosen randomly and independently with both choices being equally likely. All three frogs stop jumping as soon as two frogs arrive at the same vertex at the same time. The expected number of minutes until the frogs stop jumping is $\frac mn$ , where $m$ and $n$ are relatively prime positive integers. Find $m+n$ .

Problem 13

Circles $\omega_1$ and $\omega_2$ with radii $961$ and $625$ , respectively, intersect at distinct points $A$ and $B$ . A third circle $\omega$ is externally tangent to both $\omega_1$ and $\omega_2$ . Suppose line $AB$ intersects $\omega$ at two points $P$ and $Q$ such that the measure of minor arc $\widehat{PQ}$ is $120^{\circ}$ . Find the distance between the centers of $\omega_1$ and $\omega_2$ .

Problem 14

For any positive integer $a, \sigma(a)$ denotes the sum of the positive integer divisors of $a$ . Let $n$ be the least positive integer such that $\sigma(a^n)-1$ is divisible by $2021$ for all positive integers $a$ . Find the sum of the prime factors in the prime factorization of $n$ .

Problem 15

Let $S$ be the set of positive integers $k$ such that the two parabolas $y=x^2-k~~\text{and}~~x=2(y-20)^2-k$ intersect in four distinct points, and these four points lie on a circle with radius at most $21$ . Find the sum of the least element of $S$ and the greatest element of $S$ .

参考答案及详解注册后登录可见：

Problem1

Solution 1 Make the translation $y \rightarrow y+20$ to obtain $20+y=x^2-k , x=2y^2-k$ . Multiply the first equation by 2 and sum, we see that $2(x^2+y^2)=3k+40+2y+x$ . Completing the square gives us $(y- \frac{1}{2})^2+(x - \frac{1}{4})^2 = \frac{325+24k}{16}$ ; this explains why the two parabolas intersect at four points that lie on a circle*. For the upper bound, observe that $LHS \leq 21^2=441 \rightarrow 24k \leq 6731$ , so $k \leq 280$ .
For the lower bound, we need to ensure there are 4 intersections to begin with. (Here I'm using the un-translated coordinates.) Draw up a graph, and realize that two intersections are guaranteed, on the so called "right branch" of $y=x^2-k$ . As we increase the value of k, two more intersections appear on the "left branch." $k=4$ does not work because the "leftmost" point of $x=2(y-20)^2-4$ is $(-4,20)$ which lies to the right of $(-\sqrt{24}, 20)$ , which is on the graph $y=x^2-4$ . While technically speaking this doesn't prove that there are no intersections (why?), drawing the graph should convince you that this is the case. Clearly, no k less than 4 works either. $k=5$ does work because the two graphs intersect at $(-5,20)$ , and by drawing the graph, you realize this is not a tangent point and there is in fact another intersection nearby, due to slope. Therefore, the answer is $5+280=285$ .

In general, (Assuming four intersections exist) when two conics intersect, if one conic can be written as $ax^2+by^2=f(x,y)$ and the other as $cx^2+dy^2=g(x,y)$ for f,g polynomials of degree at most 1, whenever $(a,b),(c,d)$ are linearly independent, we can combine the two equations and then complete the square to achieve $(x-p)^2+(y-q)^2=r^2$ . We can also combine these two equations to form a parabola, or a hyperbola, or an ellipse. When $(a,b),(c,d)$ are not L.I., the intersection points instead lie on a line, which is a circle of radius infinity. When the two conics only have 3,2 or 1 intersection points, the statement that all these points lie on a circle is trivially true.

Problem2

Solution 1 (Similar Triangles)

Let $G$ be the intersection of $AD$ and $FC$ . From vertical angles, we know that $\angle FGA= \angle DGC$ . Also, given that $ABCD$ and $AFCE$ are rectangles, we know that $\angle AFG= \angle CDG=90 ^{\circ}$ . Therefore, by AA similarity, we know that triangles $AFG$ and $CDG$ are similar.
Let $AG=x$ . Then, we have $DG=11-x$ . By similar triangles, we know that $FG=\frac{7}{3}(11-x)$ and $CG=\frac{3}{7}x$ . We have $\frac{7}{3}(11-x)+\frac{3}{7}x=FC=9$ .
Solving for $x$ , we have $x=\frac{35}{4}$ . The area of the shaded region is just $3\cdot \frac{35}{4}=\frac{105}{4}$ .
Thus, the answer is $105+4=\framebox{109}$ .
~yuanyuanC

Solution 2 (Coordinate Geometry Bash)

Suppose $B=(0,0).$ It follows that $\begin{align*} A&=(0,3), \\ C&=(11,0), \\ D&=(11,3). \end{align*}$ Since $AECF$ is a rectangle, we have $AE=FC=9$ and $EC=AF=7.$ The equation of the circle with center $A$ and radius $\overline{AE}$ is $x^2+(y-3)^2=81,$ and the equation of the circle with center $C$ and radius $\overline{CE}$ is $(x-11)^2+y^2=49.$ We now have a system of two equations with two variables. Expanding and rearranging respectively give $\begin{align*} x^2+y^2-6y&=72, &(1) \\ x^2+y^2-22x&=-72. &(2) \end{align*}$ Subtracting $(2)$ from $(1),$ we get $22x-6y=144.$ Simplifying and rearranging produce $x=\frac{3y+72}{11}. \hspace{34.5mm} (*)$ Substituting $(*)$ into $(1)$ gives $\left(\frac{3y+72}{11}\right)^2+y^2-6y=72,$ which is a quadratic of $y.$ We clear fractions by multiplying both sides by $11^2=121,$ then solve by factoring: $\begin{align*} \left(3y+72\right)^2+121y^2-726y&=8712 \\ \left(9y^2+432y+5184\right)+121y^2-726y&=8712 \\ 130y^2-294y-3528&=0 \\ 2(5x+21)(13x-84)&=0 \\ y&=-\frac{21}{5},\frac{84}{13}. \end{align*}$ Since $E$ is in Quadrant IV, we have $E=\left(\frac{3\left(-\frac{21}{5}\right)+72}{11},-\frac{21}{5}\right)=\left(\frac{27}{5},-\frac{21}{5}\right).$ It follows that the equation of $\overleftrightarrow{AE}$ is $y=-\frac{4}{3}x+3.$ Let $G$ be the intersection of $\overline{AD}$ and $\overline{FC},$ and $H$ be the intersection of $\overline{AE}$ and $\overline{BC}.$ Since $H$ is the $x$ -intercept of $\overleftrightarrow{AE},$ we obtain $H=\left(\frac94,0\right).$ By symmetry, quadrilateral $AGCH$ is a parallelogram. Its area is $HC\cdot AB=\left(11-\frac94\right)\cdot3=\frac{105}{4},$ from which the requested sum is $105+4=\boxed{109}.$ ~MRENTHUSIASM

Solution 3 (Pythagorean Theorem)

Let the intersection of $AE$ and $BC$ be $G$ , and let $BG=x$ , so $CG=11-x$ .
By the Pythagorean theorem, ${AG}^2={AB}^2+{BG}^2$ , so $AG=\sqrt{x^2+9}$ , and thus $EG=9-\sqrt{x^2+9}$ .
By the Pythagorean theorem again, ${CG}^2={EG}^2+{CE}^2$ : $11-x=\sqrt{7^2+(9-\sqrt{x^2+9})^2}.$ Solving, we get $x=\frac{9}{4}$ , so the area of the parallelogram is $3\cdot(11-\frac{9}{4})=\frac{105}{4}$ , and $105+4=\framebox{109}$ .
~JulianaL25

Solution 4 (Similar triangles and area)

Again, let the intersection of $AE$ and $BC$ be $G$ . By AA similarity, $AFG \sim CDG$ with a $\frac{7}{3}$ ratio. Define $x$ as $\frac{[CDG]}{9}$ . Because of similar triangles, $[AFG] = 49x$ . Using $ABCD$ , the area of the parallelogram is $33-18x$ . Using $AECF$ , the area of the parallelogram is $63-98x$ . These equations are equal, so we can solve for $x$ and obtain $x = \frac{3}{8}$ . Thus, $18x = \frac{27}{4}$ , so the area of the parallelogram is $33 - \frac{27}{4} = \frac{105}{4}$ .
~mathboy100

Solution 5

Let $P = AD \cap FC$ , and $K = AE \cap BC$ . Also let $AP = x$ . $CK$ also has to be $x$ by parallelogram properties. Then $PD$ and $BK$ must be $11-x$ because the sum of the segments has to be $11$ .
We can easily solve for $PC$ by the Pythagorean Theorem: $\begin{align*} DC^2 + PD^2 &= PC^2\\ 9 + (11-x)^2 &= PC^2 \end{align*}$ It follows shortly that $PC = \sqrt{x^2-22x+30}$ .
Also, $FC = 9$ , and $FP + PC = 9$ . We can then say that $PC = \sqrt{x^2-22x+30}$ , so $FP = 9 - \sqrt{x^2-22x+30}$ .
Now we can apply the Pythagorean Theorem to $\triangle AFP$ . $\begin{align*} AF^2 + FP^2 = AP^2\\ 49 + \left(9 - \sqrt{x^2-22x+30}\right)^2 = x^2 \end{align*}$ This simplifies (not-as-shortly) to $x = \dfrac{35}{4}$ . Now we have to solve for the area of $APCK$ . We know that the height is $3$ because the height of the parallelogram is the same as the height of the smaller rectangle.
From the area of a parallelogram (we know that the base is $\dfrac{35}{4}$ and the height is $3$ ), it is clear that the area is $\dfrac{105}{4}$ , giving an answer of $\boxed{109}$ . ~ishanvannadil2008 for the solution sketch, Tuatara for rephrasing and $\LaTeX$ .

Solution 6 (Trigbash)

Let the intersection of $AE$ and $BC$ be $G$ . It is useful to find $\tan(\angle DAE)$ , because $\tan(\angle DAE)=\frac{3}{BG}$ and $\frac{3}{\tan(\angle DAE)}=BG$ . From there, subtracting the areas of the two triangles from the larger rectangle, we get Area = $33-3BG=33-\frac{9}{\tan(\angle DAE)}$ .
let $\angle CAD = \alpha$ . Let $\angle CAE = \beta$ . Note, $\alpha+\beta=\angle DAE$ . $\alpha=\tan^{-1}\left(\frac{3}{11}\right)$ $\beta=\tan^{-1}\left(\frac{7}{9}\right)$ $\tan(\angle DAE) = \tan\left(\tan^{-1}\left(\frac{3}{11}\right)+\tan^{-1}\left(\frac{7}{9}\right)\right) = \frac{\frac{3}{11}+\frac{7}{9}}{1-\frac{3}{11}\cdot\frac{7}{9}} = \frac{\frac{104}{99}}{\frac{78}{99}} = \frac{4}{3}$ Area = $33-\frac{9}{\frac{4}{3}} = 33-\frac{27}{4 } = \frac{105}{4}$ . The answer is $105+4=109$ . ~ twotothetenthis1024

Problem 3

Solution 1

We want to find the number of positive integers $n<1000$ which can be written in the form $n = 2^a - 2^b$ for some non-negative integers $a > b \ge 0$ (note that if $a=b$ , then $2^a-2^b = 0$ ). We first observe $a$ must be at most 10; if $a \ge 11$ , then $2^a - 2^b \ge 2^{10} > 1000$ . As $2^{10} = 1024 \approx 1000$ , we can first choose two different numbers $a > b$ from the set $\{0,1,2,\ldots,10\}$ in $\binom{11}{2}=55$ ways. This includes $(a,b) = (10,0)$ , $(10,1)$ , $(10,2)$ , $(10,3)$ , $(10,4)$ which are invalid as $2^a - 2^b > 1000$ in this case. For all other choices $a$ and $b$ , the value of $2^a - 2^b$ is less than 1000.
We claim that for all other choices of $a$ and $b$ , the values of $2^a - 2^b$ are pairwise distinct. More specifically, if $(a_1,b_1) \neq (a_2,b_2)$ where $10 \ge a_1 > b_1 \ge 0$ and $10 \ge a_2 > b_2 \ge 0$ , we must show that $2^{a_1}-2^{b_1} \neq 2^{a_2} - 2^{b_2}$ . Suppose otherwise for sake of contradiction; rearranging yields $2^{a_1}+2^{b_2} = 2^{a_2}+2^{b_1}$ . We use the fact that every positive integer has a unique binary representation:
If $a_1 \neq b_2$ then $\{a_1,b_2\} = \{a_2,b_1\}$ ; from here we can deduce either $a_1=a_2$ and $b_1=b_2$ (contradicting the assumption that $(a_1,b_1) \neq (a_2,b_2)$ , or $a_1=b_1$ and $a_2=b_2$ (contradicting the assumption $a_1>b_1$ and $a_2>b_2$ ).
If $a_1 = b_2$ then $2^{a_1}+2^{b_2} = 2 \times 2^{a_1}$ , and it follows that $a_1=a_2=b_1=b_2$ , also contradicting the assumption $(a_1,b_1) \neq (a_2,b_2)$ . Hence we obtain contradiction.*
Then there are $\binom{11}{2}-5$ choices for $(a,b)$ for which $2^a - 2^b$ is a positive integer less than 1000; by the above claim, each choice of $(a,b)$ results in a different positive integer $n$ . Then there are $55-5 = \boxed{050}$ integers which can be expressed as a difference of two powers of 2.

Note: The uniqueness of binary representation could be rather easily proven, but if you cannot convince yourself on the spot that this is the case, consider the following alternative proof. Let $(a_1,b_1) \neq (a_2,b_2)$ where $10 \ge a_1 > b_1 \ge 0$ and $10 \ge a_2 > b_2 \ge 0$ and $2^{a_1}-2^{b_1} = 2^{a_2} - 2^{b_2}$ , for the sake of contradiction. Therefore $\deg_{2}(2^{a_1}-2^{b_1})=\deg_{2}(2^{a_2}-2^{b_2})$ , or $b_1=b_2$ . Plugging in, we see that $2^{a_1}=2^{a_2}$ , or $a_1=a_2$ , contradiction.

Note by Ross Gao

Solution 2 (Casework)

Case 1: When our answer is in the form $2^n-2^i$ , where $i$ is an integer such that $0\le i\le 4$ .
We start with the subcase where it is $2^n-2^0$ , for some integer $n$ where $n>0$ (this is because the case where $n=0$ yields $2^0-2^0=0$ , which doesn't work because it must be a positive integer.) Note that $2^{10}=1024$ , and $2^9=512$ . Our answer needs to be less than $1000$ , so the maximum possible result (in this case) is $2^9-2^0$ . Our lowest result is $2^1-2^0$ . All the positive powers of two less than $1024$ work, so we have $9$ possibilities for this subcase. For subcases $i=1, i=2, i=3,$ and $i=4$ , we have $8, 7, 6,$ and $5$ possibilities, respectively. Case 2: When our answer is in the form of $2^n-2^j$ , where $j$ is an integer such that $5\le j\le 9$ .
We can start with the subcase where $j=5$ . We notice that $2^5=32$ , and $2^{10}-2^5=992$ which is less than $1000$ , so the greatest result in this subcase is actually $2^{10}-2^5$ , and the lowest is $2^6-2^5$ . Thus, we have $5$ possibilities. For the other four subcases, we have $4, 3, 2,$ and $1$ possibilities, respectively. Answer: We note that these are our only cases, as numbers in the form of $2^n-2^{10}$ and beyond are greater than $1000$ .
Thus, our result is $9+8+7+6+5+5+4+3+2+1=(9+8+7+6+5+4+3+2+1)+5=\boxed{50}$ . ~jehu26

Solution 3 (Bash)

We look for all positive integers of the form $2^a-2^b<1000,$ where $0\leq b<a.$ Performing casework on $a,$ we can enumerate all possibilities in the table below: $\begin{array}{c|c} & \\ [-2.25ex] \boldsymbol{a} & \boldsymbol{b} \\ \hline & \\ [-2ex] 1 & 0 \\ 2 & 0,1 \\ 3 & 0,1,2 \\ 4 & 0,1,2,3 \\ 5 & 0,1,2,3,4 \\ 6 & 0,1,2,3,4,5 \\ 7 & 0,1,2,3,4,5,6 \\ 8 & 0,1,2,3,4,5,6,7 \\ 9 & 0,1,2,3,4,5,6,7,8 \\ 10 & \xcancel{0},\xcancel{1},\xcancel{2},\xcancel{3},\xcancel{4},5,6,7,8,9 \\ [0.5ex] \end{array}$ As indicated by the X-marks, the ordered pairs $(a,b)=(10,0),(10,1),(10,2),(10,3),(10,4)$ generate $2^a-2^b>1000,$ which are invalid. Note that each of the remaining ordered pairs generates one unique desired positive integer. We prove this statement as follows:

1. The positive integers generated for each value of $a$ are clearly different.

1. For all integers $1\leq k\leq9,$ the largest positive integer generated for $a=k$ is $1$ less than the smallest positive integer generated for $a=k+1.$

Together, we have justified our claim in bold. Our answer is $1+2+3+4+5+6+7+8+9+5=\boxed{050}.$ ~MRENTHUSIASM

Solution 4

First, you need to notice that it is impossible to have overlapping, making the problem easier.
Case 1 : $2^0$ There are $9$ ways here, from $2^1$ to $2^9$ It is easy to see here that this continues all the way down to one. However, when the case gets to $32$ , there are 5 ways instead of 4 because $2^{10}-2^5$ is smaller than 1000.
Thus, $9+8+7+6+5+5+4+3+2+1 = 50$ So the answer is $\boxed{050}$

Problem 4

Solution 1

Suppose we have $1$ coin in the first pile. Then $(1, 2, 63), (1, 3, 62), \ldots, (1, 32, 33)$ all work for a total of $31$ piles. Suppose we have $2$ coins in the first pile, then $(2, 3, 61), (2, 4, 60), \ldots, (2, 31, 33)$ all work, for a total of $29$ . Continuing this pattern until $21$ coins in the first pile, we have the sum $31+29+28+26+25+\ldots+4+2+1=(31+28+25+22+\ldots+1)+$ $(29+26+23+\ldots+2)=176+155=\boxed{331}$ .

Solution 2

Let the three piles have $a, b, c$ coins respectively. If we disregard order, then we just need to divide by $3! = 6$ at the end.
We know $a + b + c = 66$ . Since $a, b, c$ are positive integers, there are $\binom{65}{2}$ ways from Stars and Bars.
However, we must discard the cases where $a = b$ or $a = c$ or $b = c$ . The three cases are symmetric, so we just take the first case and multiply by 3. We have $2a + c = 66 \implies a = 1, 2, \dots 32$ for 32 solutions. Multiplying by 3, we will subtract 96 from our total.
But we undercounted where $a = b = c = 22$ . This is first counted 1 time, then we subtract it 3 times, so we add it back twice. There is clearly only 1 way, for a total of 2.
Hence, the answer is $\frac{\binom{65}{2} - 96 + 2}{6} = \boxed{331}.$

Solution 3

Let the piles have $a, b$ and $c$ coins, with $0 < a < b < c$ . Then, let $b = a + k_1$ , and $c = b + k_2$ , such that each $k_i \geq 1$ . The sum is then $a + a+k_1 + a+k_1+k_2 = 66 \implies 3a+2k_1 + k_2 = 66$ . This is simply the number of positive solutions to the equation $3x+2y+z = 66$ . Now, we take cases on $a$ .
If $a = 1$ , then $2k_1 + k_2 = 63 \implies 1 \leq k_1 \leq 31$ . Each value of $k_1$ corresponds to a unique value of $k_2$ , so there are $31$ solutions in this case. Similarly, if $a = 2$ , then $2k_1 + k_2 = 60 \implies 1 \leq k_1 \leq 29$ , for a total of $29$ solutions in this case. If $a = 3$ , then $2k_1 + k_1 = 57 \implies 1 \leq k_1 \leq 28$ , for a total of $28$ solutions. In general, the number of solutions is just all the numbers that aren't a multiple of $3$ , that are less than or equal to $31$ .
We then add our cases to get $1 + 2 + 4 + 5 + \cdots + 31 = 1 + 2 + 3 + \cdots + 31 - 3(1 + 2 + 3 + \cdots + 10) = \frac{31(32)}{2} - 3(55) = 31 \cdot 16 - 165 = 496 - 165 = \boxed{331}$ as our answer.

Solution 4

We make an equation for how this is true. a+b+c = 66, where a is less than b, is less than c. We don't have a clear solution, so we'll try complimentary counting. First, let's find where a doesn't have to be less than b, which doesn't have to be less than c. We have $\dbinom{65}{2}$ =2080 by stars and bars. Now we need to subtract off the cases where it doesn't satisfy the condition.
We first by starting out with a = b. We can write that as 2b + c = 66. We can find there are 32 integer solutions to this equation. There are 32 solutions for b=c, and a = c by symmetry. We also need to subtract 2 from the 96, because we counted 22, 22, 22 3 times. We then have to divide by 6 because there are 3! ways to order the a, b, and c. Therefore, we have $\dfrac{\dbinom{65}{2}-94}{6}$ = $\dfrac{1986}{6} =$ $\boxed{331}$ ~Arcticturn

Problem 5

Solution 1

Let the terms be $a-b$ , $a$ , and $a+b$ . Then we want $(a-b)^2+a^2+(a+b)^2=ab^2$ , or $3a^2+2b^2=ab^2$ . Rearranging, we get $b^2=\frac{3a^2}{a-2}$ . Simplifying further, $b^2=3a+6+\frac{12}{a-2}$ . Looking at this second equation, since the right side must be an integer, $a-2$ must equal $\pm1, 2, 3, 4, 6, 12$ . Looking at the first equation, we see $a>2$ since $b^2$ is positive. This means we must test $a=3, 4, 5, 6, 8, 14$ . After testing these, we see that only $a=5$ and $a=14$ work which give $b=5$ and $b=7$ respectively. Thus the answer is $10+21=\boxed{031}$ . ~JHawk0224

Solution 2

Let the common difference be $d$ and let the middle term be $x$ . Then, we have that the sequence is $x-d,~x,~x+d.$ This means that the sum of the squares of the 3 terms of the sequence is $(x-d)^2+x^2+(x+d)^2=x^2-2xd+d^2+x^2+x^2+2xd+d^2=3x^2+2d^2.$ We know that this must be equal to $xd^2,$ so we can write that $3x^2+2d^2=xd^2,$ and it follows that $3x^2-xd^2+2d^2=3x^2-\left(d^2\right)x+2d^2=0.$ Now, we can treat $d$ as a constant and use the quadratic formula to get $x=\frac{d^2\pm \sqrt{d^4-4(3)(2d^2)}}{6}.$ We can factor pull $d^2$ out of the square root to get $x=\frac{d^2\pm d\sqrt{d^2-24}}{6}.$ Here, it is easy to test values of $d$ . We find that $d=5$ and $d=7$ are the only positive integer values of $d$ that make $\sqrt{d^2-24}$ a positive integer. $^{*}$ $d=5$ gives $x=5$ and $x=\frac{10}{3}$ , but we can ignore the latter. $d=7$ gives $x=14$ , as well as a fraction which we can ignore.
Since $d=5,~x=5$ and $d=7, x=14$ are the only two solutions and we want the sum of the third terms, our answer is $(5+5)+(7+14)=10+21=\boxed{031}$ . -BorealBear, minor edit by Kinglogic $^*$ To prove this, let $\sqrt{d^2-24} = k$ , then $d^2-k^2=24$ which is $(d+k)(d-k)=24,$ then remembering that $d$ and $k$ are integers see if you can figure it out. -PureSwag

Solution 3

Proceed as in solution 2, until we reach $3x^2+2d^2=xd^2,$ Write $d^2=\frac{3x^2}{x-2}$ , it follows that $x-2=3k^2$ for some (positive) integer k and $k \mid x$ .
Taking both sides modulo $k$ , $-2 \equiv 0 \pmod{k}$ , so $k \mid 2 \rightarrow k=1,2$ .
When $k=1$ , we have $x=5$ and $d=5$ . When $k=2$ , we have $x=14$ and $d=7$ . Summing the two cases, we have $10+21=\framebox{031}$ .
-Ross Gao

Solution 4 (Combining Solution 1 and Solution 3)

As in Solution 1, write the three integers in the sequence as $a-d$ , $a$ , and $a+d$ .
Then the sum of the squares of the three integers is $(a-d)^2+a^2+(a+d)^2 = 3a^2+2d^2$ .
Setting this equal to the middle term times the common difference squared, which is $ad^2$ ,
and solving for $d^2$ we get: $3a^2+2d^2 = ad^2 \implies ad^2-2d^2 = 3a^2 \implies d^2(a-2) = 3a^2 \implies d^2 = \frac{3a^2}{a-2}$ The numerator has to be positive, so the denominator has to be positive too for the sequence
to be strictly increasing; that is, $a>2$ .
For $\frac{3a^2}{a-2}$ to be a perfect square, $\frac{3}{a-2}$ must be a perfect square as well.
This means that $a-2$ is divisible by 3, and whatever left over is a perfect square.
We can express this as an equation: let the perfect square left over be $n^2$ . Then: $3n^2 = a-2$ . Now when you divide the numerator and denominator by 3, you are left with $d^2 = \frac{a^2}{n^2} \implies d = \frac{a}{n}$ . Because the sequence is of integers, d must also be an
integer, which means that $n$ must divide $a$ .
Taking the above equation we can solve for $a$ : $3n^2 = a-2 \implies a = 3n^2+2$ .
This means that $3n^2+2$ is divisible by $n$ . $3n^2$ is automatically divisible by $n$ , so $2$ must be divisible by $n$ . Then $n$ must be either of $\{1,2\}$ . Plugging back into the equation, $n = 1 \implies a = 5 \implies d = 5$ , so $a+d = 5+5 = 10$ . $n = 2 \implies a = 14 \implies d = 7$ , so $a+d = 14+7 = 21$ .
Finally, $10+21 = \boxed{031}$

Problem 6

Solution 1

First scale down the whole cube by 12. Let point P have coordinates $(x, y, z)$ , A have coordinates $(0, 0, 0)$ , and $s$ be the side length. Then we have the equations $(s-x)^2+y^2+z^2=(5\sqrt{10})^2$ $x^2+(s-y)^2+z^2=(5\sqrt{5})^2$ $x^2+y^2+(s-z)^2=(10\sqrt{2})^2$ $(s-x)^2+(s-y)^2+(s-z)^2=(3\sqrt{7})^2$ These simplify into $s^2+x^2+y^2+z^2-2sx=250$ $s^2+x^2+y^2+z^2-2sy=125$ $s^2+x^2+y^2+z^2-2sz=200$ $3s^2-2s(x+y+z)+x^2+y^2+z^2=63$ Adding the first three equations together, we get $3s^2-2s(x+y+z)+3(x^2+y^2+z^2)=575$ . Subtracting this from the fourth equation, we get $2(x^2+y^2+z^2)=512$ , so $x^2+y^2+z^2=256$ . This means $PA=16$ . However, we scaled down everything by 12 so our answer is $16*12=\boxed{192}$ . ~JHawk0224

Solution 2 (Solution 1 with slight simplification)

Once the equations for the distance between point P and the vertices of the cube have been written. We can add the first, second, and third to receive, $2(x^2 + y^2 + z^2) + (s-x)^2 + (s-y)^2 + (s-z)^2 = 250 + 125 + 200.$ Subtracting the fourth equation gives, $2(x^2 + y^2 + z^2) = 575 - 63$ $x^2 + y^2 + z^2 = 256$ $\sqrt{x^2 + y^2 + z^2} = 16.$ Since point $A = (0,0,0), PA = 16$ , and since we scaled the answer is $16 \cdot 12 = \boxed{192}$ ~Aaryabhatta1

Solution 3

Let E be the vertex of the cube such that ABED is a square. By the British Flag Theorem, we can easily we can show that $PA^2 + PE^2 = PB^2 + PD^2$ and $PA^2 + PG^2 = PC^2 + PE^2$ Hence, adding the two equations together, we get $2PA^2 + PG^2 = PB^2 + PC^2 + PD^2$ . Substituting in the values we know, we get $2PA^2 + 7\cdot 36^2 =10\cdot60^2 + 5\cdot 60^2 + 2\cdot 120^2$ .
Thus, we can solve for $PA$ , which ends up being $\boxed{192}$ .

Problem 7

Solution 1

The maximum value of $\sin \theta$ is $1$ , which is achieved at $\theta = \frac{\pi}{2}+2k\pi$ for some integer $k$ . This is left as an exercise to the reader.
This implies that $\sin(mx) = \sin(nx) = 1$ , and that $mx = \frac{\pi}{2}+2a\pi$ and $nx = \frac{\pi}{2}+2b\pi$ , for integers $a, b$ .
Taking their ratio, we have $\frac{mx}{nx} = \frac{\frac{\pi}{2}+2a\pi}{\frac{\pi}{2}+2b\pi} \implies \frac{m}{n} = \frac{4a + 1}{4b + 1} \implies \frac{m}{4a + 1} = \frac{n}{4b + 1} = k.$ It remains to find all $m, n$ that satisfy this equation.
If $k = 1$ , then $m \equiv n \equiv 1 \pmod 4$ . This corresponds to choosing two elements from the set $\{1, 5, 9, 13, 17, 21, 25, 29\}$ . There are $\binom 82$ ways to do so.
If $k < 1$ , by multiplying $m$ and $n$ by the same constant $c = \frac{1}{k}$ , we have that $mc \equiv nc \equiv 1 \pmod 4$ . Then either $m \equiv n \equiv 1 \pmod 4$ , or $m \equiv n \equiv 3 \pmod 4$ . But the first case was already counted, so we don't need to consider that case. The other case corresponds to choosing two numbers from the set $\{3, 7, 11, 15, 19, 23, 27\}$ . There are $\binom 72$ ways here.
Finally, if $k > 1$ , note that $k$ must be an integer. This means that $m, n$ belong to the set $\{k, 5k, 9k, \dots\}$ , or $\{3k, 7k, 11k, \dots\}$ . Taking casework on $k$ , we get the sets $\{2, 10, 18, 26\}, \{6, 14, 22, 30\}, \{4, 20\}, \{12, 28\}$ . Some sets have been omitted; this is because they were counted in the other cases already. This sums to $\binom 42 + \binom 42 + \binom 22 + \binom 22$ .
In total, there are $\binom 82 + \binom 72 + \binom 42 + \binom 42 + \binom 22 + \binom 22 = \boxed{63}$ pairs of $(m, n)$ .
This solution was brought to you by ~Leonard_my_dude~

Solution 2

In order for $\sin(mx) + \sin(nx) = 2$ , $\sin(mx) = \sin(nx) = 1$ .
This happens when $mx \equiv nx \equiv \frac{\pi}{2} ($ mod $2\pi).$ This means that $mx = \frac{\pi}{2} + 2\pi\alpha$ and $nx = \frac{\pi}{2} + 2\pi\beta$ for any integers $\alpha$ and $\beta$ .
As in Solution 1, take the ratio of the two equations: $\frac{mx}{nx} = \frac{\frac{\pi}{2}+2\pi\alpha}{\frac{\pi}{2}+2\pi\beta} \implies \frac{m}{n} = \frac{\frac{1}{2}+2\alpha}{\frac{1}{2}+2\beta} \implies \frac{m}{n} = \frac{4\alpha+1}{4\beta+1}$ Now notice that the numerator and denominator of $\frac{4\alpha+1}{4\beta+1}$ are both odd, which means that $m$ and $n$ have the same power of two (the powers of 2 cancel out).
Let the common power be $p$ : then $m = 2^p\cdot a$ , and $n = 2^p\cdot b$ where $a$ and $b$ are integers between 1 and 30.
We can now rewrite the equation: $\frac{2^p\cdot a}{2^p\cdot b} = \frac{4\alpha+1}{4\beta+1} \implies \frac{a}{b} = \frac{4\alpha+1}{4\beta+1}$ Now it is easy to tell that $a \equiv 1 ($ mod $4)$ and $b \equiv 1 ($ mod $4)$ . However, there is another case: that $a \equiv 3 ($ mod $4)$ and $b \equiv 3 ($ mod $4)$ . This is because multiplying both $4\alpha+1$ and $4\beta+1$ by $-1$ will not change the fraction, but each congruence will be changed to $-1 ($ mod $4) \equiv 3 ($ mod $4)$ .
From the first set of congruences, we find that $a$ and $b$ can be two of $\{1, 5, 9, \cdots, 29\}$ .
From the second set of congruences, we find that $a$ and $b$ can be two of $\{3, 7, 11, \cdots, 27\}$ .
Now all we have to do is multiply by $2^p$ to get back to $m$ and $n$ . Let’s organize the solutions in order of increasing values of $p$ , keeping in mind that $m$ and $n$ are bounded between 1 and 30.
For $p = 0$ we get $\{1, 5, 9, \cdots, 29\}, \{3, 7, 11, \cdots, 27\}$ .
For $p = 1$ we get $\{2, 10, 18, 26\}, \{6, 14, 22, 30\}$ For $p = 2$ we get $\{4, 20\}, \{12, 28\}$ If we increase the value of $p$ more, there will be less than two integers in our sets, so we are done there.
There are 8 numbers in the first set, 7 in the second, 4 in the third, 4 in the fourth, 2 in the fifth, and 2 in the sixth.
In each of these sets we can choose 2 numbers to be $m$ and $n$ and then assign them in increasing order. Thus there are: $\dbinom{8}{2}+\dbinom{7}{2}+\dbinom{4}{2}+\dbinom{4}{2}+\dbinom{2}{2}+\dbinom{2}{2}$ $= 28+21+6+6+1+1 = \boxed{63}$ possible pairings of $m, n$ that satisfy the conditions.
-KingRavi

Solution 3

We know that the range of $sin$ is between $-1$ and $1$ .
Thus, the only way for the sum to be $2$ is for $sin$ of $mx$ and $nx$ to both be $1$ .
The $sin$ of $(90+360k)$ is equal to 1.
Assuming $mx$ and $nm$ are both positive, m and n could be $1,5,9,13,17,21,25,29$ . There are $8$ ways, so $\dbinom{8}{2}$ .
If bother are negative, m and n could be $3,7,11,15,19,23,27$ . There are $7$ ways, so $\dbinom{7}{2}$ .
However, the pair $(1,5)$ could also be $(2, 10)$ and so on. The same goes for some other pairs.
In total there are $14$ of these extra pairs.
The answer is $28+21+14 = \boxed{063}$

Problem 8

Solution 1

Let $y = |x|.$ Then the equation becomes $\left|\left|20y-y^2\right|-c\right| = 21$ , or $\left|y^2-20y\right| = c \pm 21$ . Note that since $y = |x|$ , $y$ is nonnegative, so we only care about nonnegative solutions in $y$ . Notice that each positive solution in $y$ gives two solutions in $x$ ( $x = \pm y$ ), whereas if $y = 0$ is a solution, this only gives one solution in $x$ , $x = 0$ . Since the total number of solutions in $x$ is even, $y = 0$ must not be a solution. Hence, we require that $\left|y^2-20y\right| = c \pm 21$ has exactly $6$ positive solutions and is not solved by $y = 0.$ If $c < 21$ , then $c - 21$ is negative, and therefore cannot be the absolute value of $y^2 - 20y$ . This means the equation's only solutions are in $\left|y^2-20y\right| = c + 21$ . There is no way for this equation to have $6$ solutions, since the quadratic $y^2-20y$ can only take on each of the two values $\pm(c + 21)$ at most twice, yielding at most $4$ solutions. Hence, $c \ge 21$ . $c$ also can't equal $21$ , since this would mean $y = 0$ would solve the equation. Hence, $c > 21.$ At this point, the equation $y^2-20y = c \pm 21$ will always have exactly $2$ positive solutions, since $y^2-20y$ takes on each positive value exactly once when $y$ is restricted to positive values (graph it to see this), and $c \pm 21$ are both positive. Therefore, we just need $y^2-20y = -(c \pm 21)$ to have the remaining $4$ solutions exactly. This means the horizontal lines at $-(c \pm 21)$ each intersect the parabola $y^2 - 20y$ in two places. This occurs when the two lines are above the parabola's vertex $(10,-100)$ . Hence we have: $-(c + 21) > -100$ $c + 21 < 100$ $c < 79$ Hence, the integers $c$ satisfying the conditions are those satisfying $21 < c < 79.$ There are $\boxed{057}$ such integers. Note: Be careful of counting at the end, you may mess up and get 59.

Solution 2 (also graphing)

Graph $y=|20|x|-x^2|$ (If you are having trouble, look at the description in the next two lines and/or the diagram in solution 3). Notice that we want this to be equal to $c-21$ and $c+21$ .
We see that from left to right, the graph first dips from very positive to $0$ at $x=-20$ , then rebounds up to $100$ at $x=-10$ , then falls back down to $0$ at $x=0$ .
The positive $x$ are symmetric, so the graph re-ascends to $100$ at $x=10$ , falls back to $0$ at $x=10$ , and rises to arbitrarily large values afterwards.
Now we analyze the $y$ (varied by $c$ ) values. At $y=k<0$ , we will have no solutions, as the line $y=k$ will have no intersections with our graph.
At $y=0$ , we will have exactly $3$ solutions for the three zeroes.
At $y=n$ for any $n$ strictly between $0$ and $100$ , we will have exactly $6$ solutions.
At $y=100$ , we will have $4$ solutions, because local maxima are reached at $x= \pm 10$ .
At $y=m>100$ , we will have exactly $2$ solutions.
To get $12$ distinct solutions for $y=|20|x|-x^2|=c \pm 21$ , both $c +21$ and $c-21$ must produce $6$ solutions.
Thus $0<c-21$ and $c+21<100$ , so $c \in \{ 22, 23, \dots , 77, 78 \}$ is required.
It is easy to verify that all of these choices of $c$ produce $12$ distinct solutions (none overlap), so our answer is $\boxed{057}$ .

Solution 3 (Piecewise Functions: Analyses and Graphs)

We take cases for the outermost absolute value, then rearrange: $\left|20|x|-x^2\right|-c=\pm21.$ Let $f(x)=\left|20|x|-x^2\right|.$ We will rewrite $f(x)$ as a piecewise function without using any absolute value: $f(x) = \begin{cases} \left|-20x-x^2\right| & \mathrm{if} \ x \le 0 \begin{cases} 20x+x^2 & \mathrm{if} \ x\le-20 \\ -20x-x^2 & \mathrm{if} \ -20<x\leq0 \end{cases} \\ \left|20x-x^2\right| & \mathrm{if} \ x > 0 \begin{cases} 20x-x^2 & \mathrm{if} \ 0<x\leq20 \\ -20x+x^2 & \mathrm{if} \ x>20 \end{cases} \end{cases}.$ We graph $f(x)$ with all extremum points labeled, as shown below. The fact that $f(x)$ is an even function ( $f(x)=f(-x)$ holds for all real numbers $x,$ so the graph of $f(x)$ is symmetric about the $y$ -axis) should facilitate the process of graphing.

Graph in Desmos: https://www.desmos.com/calculator/tdbbceyb9f Since $【全网首发】2021AIME I 真题及答案$ has $12$ distinct real solutions, it is clear that each case has $6$ distinct real solutions geometrically. We shift the graph of $f(x)$ down by $c$ units, where $c>0:$

For $f(x)-c=21$ to have $6$ distinct real solutions, we need $0<c<79.$

For $f(x)-c=-21$ to have $6$ distinct real solutions, we need $21<c<121.$

Taking the intersection of these two cases gives $21<c<79,$ from which there are $79-21-1=\boxed{057}$ such integers $c.$ ~MRENTHUSIASM

Solution 4

Removing the absolute value bars from the equation successively, we get $\left||20|x|-x^2|-c\right|=21$ $|20|x|-x^2|= c \pm21$ $20|x|-x^2 = \pm c \pm 21$ $x^2 \pm 20x \pm c \pm21 = 0$ The discriminant of this equation is $\sqrt{400-4(\pm c \pm 21)}$ Equating the discriminant to $0$ , we see that there will be two distinct solutions to each of the possible quadratics above only in the interval $-79 < c < 79$ . However, the number of zeros the equation $ax^2+b|x|+k$ has is determined by where $ax^2+bx+k$ and $ax^2-bx+k$ intersect, namely at $(0,k)$ . When $k<0$ , $a>0$ , $ax^2+b|x|+k$ will have only $2$ solutions, and when $k>0$ , $a>0$ , then there will be $4$ real solutions, if they exist at all. In order to have $12$ solutions here, we thus need to ensure $-c+21<0$ , so that exactly $2$ out of the $4$ possible equations of the form $ax^2+b|x|+k$ given above have y-intercepts below $0$ and only $2$ real solutions, while the remaining $2$ equations have $4$ solutions. This occurs when $c>21$ , so our final bounds are $21<c<79$ , giving us $\boxed{057}$ valid values of $c$ .

Problem 9

Solution 1

Construct your isosceles trapezoid. Let, for simplicity, $AB = a$ , $AD = BC = b$ , and $CD = c$ . Extend the sides $BC$ and $AD$ mark the intersection as $P$ . Following what the question states, drop a perpendicular from $A$ to $BC$ labeling the foot as $G$ . Drop another perpendicular from $A$ to $CD$ , calling the foot $E$ . Lastly, drop a perpendicular from $A$ to $BD$ , labeling it $F$ . In addition, drop a perpendicular from $B$ to $AC$ calling its foot $F'$ .
--DIAGRAM COMING SOON--
Start out by constructing a triangle $ADH$ congruent to $\triangle ABC$ with its side of length $a$ on line $DE$ . This works because all isosceles triangles are cyclic and as a result, $\angle ADC + \angle ABC = 180^\circ$ .
Notice that $\triangle AGC \sim \triangle BF'C$ by AA similarity. We are given that $AG = 15$ and by symmetry we can deduce that $F'B = 10$ . As a result, $\frac{BF}{AG} = \frac{BC}{AC} = \frac{3}{2}$ . This gives us that $AC = BD = \frac{3}{2} b$ .
The question asks us along the lines of finding the area, $K$ , of the trapezoid $ABCD$ . We look at the area of $ABC$ and notice that it can be represented as $\frac{1}{2} \cdot AC \cdot 10 = \frac{1}{2} \cdot a \cdot 18$ . Substituting $AC = \frac{3}{2} b$ , we solve for $a$ , getting $a = \frac{5}{6} b$ .
Now let us focus on isosceles triangle $ACH$ , where $AH = AC = \frac{3}{2} b$ . Since, $AE$ is an altitude from $A$ to $CH$ of an isosceles triangle, $HE$ must be equal to $EC$ . Since $DH = a$ and $DC = c$ , we can solve to get that $DE = \frac{c-a}{2}$ and $EC = \frac{a+c}{2}$ .
We must then set up equations using the Pythagorean Theorem, writing everything in terms of $a$ , $b$ , and $c$ . Looking at right triangle $AEC$ we get $324 + \frac{(a + c)^2}{4} = \frac{9}{4} b^2$ Looking at right triangle $AED$ we get $b^2 - 324 = \frac{(c-a)^2}{4}$ Now rearranging and solving, we get two equation $a+c = 3\sqrt{b^2 - 144}$ $c - a = 2\sqrt{b^2 - 324}$ Those are convenient equations as $c+a - (c-a) = 2a = \frac{5}{3} b$ which gives us $3\sqrt{b^2 - 324} - 2\sqrt{b^2 - 324} = \frac{5}{3} b$ After some "smart" calculation, we get that $b = \frac{27}{\sqrt{2}}$ .
Notice that the question asks for $K\sqrt{2}$ , and $K = \frac{1}{2} \cdot 18 \cdot (a+c)$ by applying the trapezoid area formula. Fortunately, this is just $27\sqrt{b^2 - 144}$ , and plugging in the value of $b = \frac{27}{\sqrt{2}}$ , we get that $K\sqrt{2} = \boxed{567}$ .
~Math_Genius_164

Solution 2 (LOC and Trig)

Call AD and BC $a$ . Draw diagonal AC and call the foot of the perpendicular from B to AC $G$ . Call the foot of the perpendicular from A to line BC F, and call the foot of the perpindicular from A to DC H. Triangles CBG and CAF are similar, and we get that $【全网首发】2021AIME I 真题及答案$ Therefore, $AC=1.5a$ . It then follows that triangles ABF and ADH are similar. Using similar triangles, we can then find that $AB=\frac{5}{6}a$ . Using the Law of Cosine on ABC, We can find that the cosine of angle ABC is $-\frac{1}{3}$ . Since angles ABF and ADH are equivalent and supplementary to angle ABC, we know that the cosine of angle ADH is 1/3. It then follows that $a=\frac{27\sqrt{2}}{2}$ . Then it can be found that the area $K$ is $\frac{567\sqrt{2}}{2}$ . Multiplying this by $\sqrt{2}$ , the answer is $\boxed{567}$ . -happykeeper

Solution 3 (Similarity)

Let the foot of the altitude from A to BC be P, to CD be Q, and to BD be R.
Note that all isosceles trapezoids are cyclic quadrilaterals; thus, $A$ is on the circumcircle of $\triangle BCD$ and we have that $PRQ$ is the Simson Line from $A$ . As $\angle QAB = 90^\circ$ , we have that $\angle QAR = 90^\circ - \angle RAB =\angle ABR = \angle APR = \angle APQ$ , with the last equality coming from cyclic quadrilateral $APBR$ . Thus, $\triangle QAR \sim \triangle QPA$ and we have that $\frac{AQ}{AR} = \frac{PQ}{PA}$ or that $\frac{18}{10} = \frac{QP}{15}$ , which we can see gives us that $QP = 27$ . Further ratios using the same similar triangles gives that $QR = \frac{25}{3}$ and $RP = \frac{56}{3}$ .
We also see that quadrilaterals $APBR$ and $ARDQ$ are both cyclic, with diameters of the circumcircles being $AB$ and $AQ$ respectively. The intersection of the circumcircles are the points $A$ and $R$ , and we know $DRB$ and $QRP$ are both line segments passing through an intersection of the two circles with one endpoint on each circle. By Fact 5, we know then that there exists a spiral similarity with center A taking $\triangle APQ$ to $\triangle APD$ . Because we know a lot about $\triangle APQ$ but very little about $\triangle APD$ and we would like to know more, we wish to find the ratio of similitude between the two triangles.
To do this, we use the one number we have for $\triangle APD$ : we know that the altitude from $A$ to $BD$ has length 10. As the two triangles are similar, if we can find the height from $A$ to $PQ$ , we can take the ratio of the two heights as the ratio of similitude. To do this, we once again note that $QP = 27$ . Using this, we can drop the altitude from $A$ to $QP$ and let it intersect $QP$ at $H$ . Then, let $QH = x$ and thus $HP=27-x$ . We then have by the Pythagorean Theorem on $\triangle AQH$ and $\triangle APH$ : $15^2 - x^2 = 18^2 - (27-x)^2$ $225 - x^2 = 324 - (x^2-54x+729)$ $54x = 630$ $x=\frac{35}{3}$ Then, $RH = QH - QR = \frac{35}{3} - \frac{25}{3} = \frac{10}{3}$ . This gives us then from right triangle $\triangle ARH$ that $AH = \frac{20\sqrt{2}}{3}$ and thus the ratio of $\triangle APQ$ to $\triangle ABD$ is $\frac{3\sqrt{2}}{4}$ . From this, we see then that $AB = AP * \frac{3\sqrt{2}}{4} = 15 * \frac{3\sqrt{2}}{4} = \frac{45\sqrt{2}}{4}$ and $AD = AQ * \frac{3\sqrt{2}}{4} = 18 * \frac{3\sqrt{2}}{4} = \frac{27\sqrt{2}}{2}$ The Pythagorean Theorem on $\triangle AQD$ then gives that $QD = \sqrt{AD^2 - AQ^2} = \sqrt{(\frac{27\sqrt{2}}{2})^2 - 18^2} = \sqrt{\frac{81}{2}} = \frac{9\sqrt{2}}{2}$ Then, we have the height of trapezoid $ABCD$ is $AQ = 18$ , the top base is $AB = \frac{45\sqrt{2}}{4}$ , and the bottom base is $CD = \frac{45\sqrt{2}}{4} + 2*\frac{9\sqrt{2}}{2}$ . From the equation of a trapezoid, $K = \frac{b_1+b_2}{2} h = \frac{63\sqrt{2}}{4} * 18 = \frac{567\sqrt{2}}{2}$ , so the answer is $K\sqrt{2} = \boxed{567}$ .
- lvmath

Solution 4 (Cool Solution by advanture)

First, draw the diagram. Then, notice that since $ABCD$ is isosceles, $\Delta ABD \cong \Delta BAC$ , and the length of the altitude from $B$ to $AC$ is also $10$ . Let the foot of this altitude be $F$ , and let the foot of the altitude from $A$ to $BC$ be denoted as $E$ . Then, $\Delta BCF \sim \Delta ACE$ . So, $\frac{BC}{AC} = \frac{BF}{AE} = \frac{2}{3}$ . Now, notice that $[ABC] = \frac{10 \times AC} {2} = \frac{AB \times 18}{2} \implies AC = \frac{9 \times AB}{5}$ , where $[ABC]$ denotes the area of triangle $ABC$ . Letting $AB = x$ , this equality becomes $AC = \frac{9x}{5}$ . Also, from $\frac{BC}{AC} = \frac{2}{3}$ , we have $BC = \frac{6x}{5}$ . Now, by the Pythagorean theorem on triangles $ABF$ and $CBF$ , we have $AF = \sqrt{x^{2}-100}$ and $CF = \sqrt{ \left( \frac{6x}{5} \right) ^{2}-100}$ . Notice that $AC = AF + CF$ , so $\frac{9x}{5} = \sqrt{x^{2}-100} + \sqrt{ \left( \frac{6x}{5} \right) ^{2}-100}$ . Squaring both sides of the equation once, moving $x^{2}-100$ and $\left( \frac{6x}{5} \right) ^{2}-100$ to the right, dividing both sides by $2$ , and squaring the equation once more, we are left with $\frac{32x^{4}}{25} = 324x^{2}$ . Dividing both sides by $x^{2}$ (since we know $x$ is positive), we are left with $\frac{32x^{2}}{25} = 324$ . Solving for $x$ gives us $x = \frac{45}{2\sqrt{2}}$ .
Now, let the foot of the perpendicular from $A$ to $CD$ be $G$ . Then let $DG = y$ . Let the foot of the perpendicular from $B$ to $CD$ be $H$ . Then, $CH$ is also equal to $y$ . Notice that $ABHG$ is a rectangle, so $GH = x$ . Now, we have $CG = GH + CH = x + y$ . By the Pythagorean theorem applied to $\Delta AGC$ , we have $(x+y)^{2}+18^{2}= \left( \frac{9x}{5} \right) ^{2}$ . We know that $\frac{9x}{5} = \frac{9}{5} \cdot \frac{45}{2\sqrt{2}} = \frac{81}{2\sqrt{2}}$ , so we can plug this into this equation. Solving for $x+y$ , we get $x+y=\frac{63}{2\sqrt{2}}$ .
Finally, to find $[ABCD]$ , we use the formula for the area of a trapezoid: $K = [ABCD] = \frac{b_{1}+b_{2}}{2} \cdot h = \frac{AB+CD}{2} \cdot 18 = \frac{x+(CG+DG)}{2} \cdot 18 = \frac{2x+2y}{2} \cdot 18 = (x+y) \cdot 18 = \frac{63}{2\sqrt{2}} \cdot 18 = \frac{567}{\sqrt{2}}$ . The problem asks us for $K \cdot \sqrt{2}$ , which comes out to be $\boxed{567}$ .
~advanture

Solution 5 (Compact similarity solution)

Let $E,F,$ and $G$ be the feet of the altitudes from $A$ to $BC,CD,$ and $DB$ , respectively.
Claim: We have $2$ pairs of similar right triangles: $\triangle AEB \sim \triangle AFD$ and $\triangle AGD \sim \triangle AEC$ .
Proof: Note that $ABCD$ is cyclic. We need one more angle, and we get this from this cyclic quad: $\angle ABE = 180^\circ - \angle ABC =\angle ADC = \angle ADG$ $\angle ADG = \angle ADB =\angle ACB = \angle ACE \square$ Let $AD=a$ . We obtain from the similarities $AB = \frac{5a}{6}$ and $AC=BD=\frac{3a}{2}$ .
By Ptolemy, $(\frac{3a}{2})^2 = a^2 + \frac{5a}{6} \cdot CD$ , so $\frac{5a^2}{4} = \frac{5a}{6} \cdot CD$ .
We obtain $CD=\frac{3a}{2}$ , so $DF=\frac{CD-AB}{2}=\frac{a}{3}$ .
Applying the Pythagorean theorem on $\triangle ADF$ , we get $324=a^2 - \frac{a^2}{9}=\frac{8a^2}{9}$ .
Thus, $a=\frac{27}{\sqrt{2}}$ , and $[ABCD]=\frac{AB+CD}{2} \cdot 18 = \frac{\frac{5a}{6} +\frac{9a}{6}}{2} \cdot 18 = 18 \cdot \frac{7}{6} \cdot \frac{27}{\sqrt{2}} = \frac{567}{\sqrt{2}}$ , yielding $\boxed{567}$ .

Solution 6 (Two Variables, Two Equations)

Let $\overline{AE}, \overline{AF},$ and $\overline{AG}$ be the perpendiculars from $A$ to $\overleftrightarrow{BC}, \overleftrightarrow{CD},$ and $\overleftrightarrow{BD},$ respectively. Next, let $H$ be the intersection of $\overline{AF}$ and $\overline{BD}.$ We set $AB=x$ and $AH=y,$ as shown below.

From here, we obtain $HF=18-y$ by segment subtraction, and $BG=\sqrt{x^2-10^2}$ and $HG=\sqrt{y^2-10^2}$ by the Pythagorean Theorem.
Since $\angle ABG$ and $\angle HAG$ are both complementary to $\angle AHB,$ we have $\angle ABG = \angle HAG,$ from which $\triangle ABG \sim \triangle HAG$ by AA. It follows that $\frac{BG}{AG}=\frac{AG}{HG}\implies BG\cdot HG=AG^2,$ or $\sqrt{x^2-10^2}\cdot\sqrt{y^2-10^2}=10^2. \hspace{10mm} (1)$ Since $\angle AHB = \angle FHD$ by vertical angles, we have $\triangle AHB \sim \triangle FHD$ by AA, with the ratio of similitude $\frac{AH}{FH}=\frac{y}{18-y}.$ It follows that $DF=x\cdot\frac{18-y}{y}.$ Since $\angle EBA = \angle ECD = \angle FDA$ by angle chasing, we have $\triangle EBA \sim \triangle FDA$ by AA, with the ratio of similitude $\frac{EA}{FA}=\frac{15}{18}=\frac{5}{6}.$ It follows that $DA=\frac{6}{5}x.$ By the Pythagorean Theorem on right $\triangle ADF,$ we have $DF^2+AF^2=AD^2,$ or $\left(x\cdot\frac{18-y}{y}\right)^2+18^2=\left(\frac{6}{5}x\right)^2. \hspace{7mm} (2)$ Solving this system of equations ( $(1)$ and $(2)$ ), we get $x=\frac{45\sqrt2}{4}$ and $y=\frac{90}{7},$ so $AB=x=\frac{45\sqrt2}{4}$ and $CD=AB+2DF=x+2\left(x\cdot\frac{18-y}{y}\right)=\frac{81\sqrt2}{4}.$ Finally, the area of $ABCD$ is $K=\frac{AB+CD}{2}\cdot AF=\frac{567\sqrt2}{2},$ from which $\sqrt2 \cdot K=\boxed{567}.$

Problem 10

Solution 1

We know that $a_{1}=\tfrac{t}{t+1}$ when $t=2020$ so $1$ is a possible value of $j$ . Note also that $a_{2}=\tfrac{2038}{2040}=\tfrac{1019}{1020}=\tfrac{t}{t+1}$ for $t=1019$ . Then $a_{2+q}=\tfrac{1019+18q}{1020+19q}$ unless $1019+18q$ and $1020+19q$ are not relatively prime which happens when $q+1$ divides $18q+1019$ or $q+1$ divides $1001$ , so the least value of $q$ is $6$ and $j=2+6=8$ . We know $a_{8}=\tfrac{1019+108}{1020+114}=\tfrac{1127}{1134}=\tfrac{161}{162}$ . Now $a_{8+q}=\tfrac{161+18q}{162+19q}$ unless $18q+161$ and $19q+162$ are not relatively prime which happens the first time $q+1$ divides $18q+161$ or $q+1$ divides $143$ or $q=10$ , and $j=8+10=18$ . We have $a_{18}=\tfrac{161+180}{162+190}=\tfrac{341}{352}=\tfrac{31}{32}$ . Now $a_{18+q}=\tfrac{31+18q}{32+19q}$ unless $18q+31$ and $19q+32$ are not relatively prime. This happens the first time $q+1$ divides $18q+31$ implying $q+1$ divides $13$ , which is prime so $q=12$ and $j=18+12=30$ . We have $a_{30}=\tfrac{31+216}{32+228}=\tfrac{247}{260}=\tfrac{19}{20}$ . We have $a_{30+q}=\tfrac{18q+19}{19q+20}$ , which is always reduced by EA, so the sum of all $j$ is $1+2+8+18+30=\boxed{059}$ .

Solution 2 (Euclidean Algorithm and Generalization)

Let $a_{j_1}, a_{j_2}, a_{j_3}, \cdots, a_{j_u}$ be all terms in the form $\frac{t}{t+1},$ where $j_1<j_2<j_3<\cdots<j_u,$ and $t$ is some positive integer. We wish to find $\sum_{i=1}^{u}{j_i}.$ Suppose $a_{j_i}=\frac{m}{m+1}$ for some positive integer $m.$ To find $\boldsymbol{a_{j_{i+1}},}$ we look for the smallest positive integer $\boldsymbol{k'}$ for which $\boldsymbol{a_{j_{i+1}}=a_{j_i+k'}=\frac{m+18k'}{m+1+19k'}}$ is reducible: If $\frac{m+18k'}{m+1+19k'}$ is reducible, then there exists a common factor $d>1$ for $m+18k'$ and $m+1+19k'.$ By the Euclidean Algorithm, we have $\begin{align*} d|m+18k' \text{ and } d|m+1+19k' &\implies d|k'+1 \text{ and } d|m+18k' \\ &\implies d|k'+1 \text{ and } d|m-18. \end{align*}$ Since $m-18$ and $k'+1$ are not relatively prime, and $m$ is fixed, the smallest value of $k'$ such that $\frac{m+18k'}{m+1+19k'}$ is reducible occurs when $k'+1$ is the smallest prime factor of $m-18.$ We will prove that for such value of $\boldsymbol{k',}$ the number $\boldsymbol{a_{j_{i+1}}}$ can be written in the form $\boldsymbol{\frac{t}{t+1}:}$ $a_{j_{i+1}}=a_{j_i+k'}=\frac{m+18k'}{m+1+19k'}=\frac{(m-18)+18(k'+1)}{(m-18)+19(k'+1)}=\frac{\frac{m-18}{k'+1}+18}{\frac{m-18}{k'+1}+19}, \hspace{10mm} (*)$ where $t=\frac{m-18}{k'+1}+18$ must be a positive integer.
We start with $m=2020$ and $a_{j_1}=a_1=\frac{2020}{2021},$ then find $a_{j_2}, a_{j_3}, \cdots, a_{j_u}$ by filling out the table below recursively: $\begin{array}{c|c|c|c|c|c} & & & & & \\ [-2ex] \boldsymbol{i} & \boldsymbol{m} & \boldsymbol{m-18} & \boldsymbol{k'+1} & \boldsymbol{k'} & \boldsymbol{a_{j_{i+1}} \left(\textbf{by } (*)\right)} \\ [0.5ex] \hline\hline & & & & & \\ [-1.5ex] 1 & 2020 & 2002 & 2 & 1 & \hspace{4.25mm} a_2 = \frac{1019}{1020} \\ [1ex] 2 & 1019 & 1001 & 7 & 6 & \hspace{2.75mm} a_8 = \frac{161}{162} \\ [1ex] 3 & 161 & 143 & 11 & 10 & a_{18} = \frac{31}{32} \\ [1ex] 4 & 31 & 13 & 13 & 12 & a_{30} = \frac{19}{20} \\ [1ex] 5 & 19 & 1 & \text{N/A} & \text{N/A} & \text{N/A} \\ [1ex] \end{array}$ As $\left(j_1,j_2,j_3,j_4,j_5\right)=(1,2,8,18,30),$ the answer is $\sum_{i=1}^{5}{j_i}=\boxed{059}.$ Remark Alternatively, from $(*)$ we can set $\frac{m+18k'}{m+1+19k'}=\frac{t}{t+1}.$ We cross-multiply, rearrange, and apply Simon's Favorite Factoring Trick to get $\left(k'+1\right)(t-18)=m-18.$ Since $k'+1\geq2,$ to find the smallest $k',$ we need $k'+1$ to be the smallest prime factor of $m-18.$ Now we continue with the last two paragraphs of the solution above.

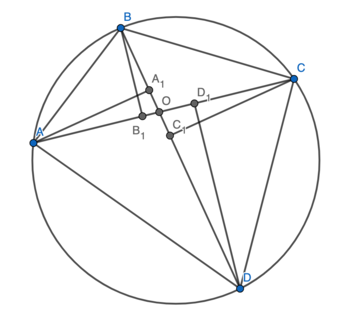
Problem 11

Solution 1

Let $O$ be the intersection of $AC$ and $BD$ . Let $\theta = \angle AOB$ .
Firstly, since $\angle AA_1D = \angle AD_1D = 90^\circ$ , we deduce that $AA_1D_1D$ is cyclic. This implies that $\triangle A_1OD_1 \sim \triangle AOD$ , with a ratio of $\frac{A_1O}{AO} = \cos \angle A_1OA = \cos \theta$ . This means that $\frac{A_1D_1}{AD} = \cos \theta$ . Similarly, $\frac{A_1B_1}{AB} = \frac{B_1C_1}{BC} = \frac{C_1D_1}{CD} = \cos \theta$ . Hence $A_1B_1 + B_1C_1 + C_1D_1 + D_1A_1 = (AB + BC + CD + DA)\cos \theta$ It therefore only remains to find $\cos \theta$ .
From Ptolemy's theorem, we have that $(BD)(AC) = 4\times6+5\times7 = 59$ . From Brahmagupta's Formula, $[ABCD] = \sqrt{(11-4)(11-5)(11-6)(11-7)} = 2\sqrt{210}$ . But the area is also $\frac{1}{2}(BD)(AC)\sin\theta = \frac{59}{2}\sin\theta$ , so $\sin \theta = \frac{4\sqrt{210}}{59} \implies \cos \theta = \frac{11}{59}$ . Then the desired fraction is $(4+5+6+7)\cos\theta = \frac{242}{59}$ for an answer of $\boxed{301}$ .

Solution 2 (Finding cos{x})

The angle $\theta$ between diagonals satisfies $\tan{\frac{\theta}{2}}=\sqrt{\frac{(s-b)(s-d)}{(s-a)(s-c)}}$ (see https://en.wikipedia.org/wiki/Cyclic_quadrilateral#Angle_formulas). Thus, $\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-4)(11-6)}{(11-5)(11-7)}}$ or $\tan{\frac{\theta}{2}}=\sqrt{\frac{(11-5)(11-7)}{(11-4)(11-6)}}$ That is, $\tan^2{\frac{\theta}{2}}=\frac{1-\cos^2{\frac{\theta}{2}}}{\cos^2{\frac{\theta}{2}}}=\frac{24}{35}$ or $\frac{35}{24}$ Thus, $\cos^2{\frac{\theta}{2}}=\frac{35}{59}$ or $\frac{24}{59}$ $\cos{\theta}=2\cos^2{\frac{\theta}{2}}-1=\frac{\pm11}{59}$ In this context, $\cos{\theta}>0$ . Thus, $\cos{\theta}=\frac{11}{59}$ $Ans=22*\cos{\theta}=22*\frac{11}{59}=\frac{242}{59}=\frac{m}{n}$ $m+n=242+59=\boxed{301}$ ~y.grace.yu

Solution 3 (Pythagorean Theorem)

We assume that the two quadrilateral mentioned in the problem are similar (due to both of them being cyclic). Note that by Ptolemy’s, one of the diagonals has length $\sqrt{4 \cdot 6 + 5 \cdot 7} = \sqrt{59}.$ WLOG we focus on diagonal $BD.$ To find the diagonal of the inner quadrilateral, we drop the altitude from $A$ and $C$ and calculate the length of $A_1C_1.$ Let $x$ be $A_1D$ (Thus $A_1B = \sqrt{59} - x.$ By Pythagorean theorem, we have $49 - x^2 = 16 - (\sqrt{59} - x)^2 \implies 92 = 2\sqrt{59}x \implies x = \frac{46}{\sqrt{59}} = \frac{46\sqrt{59}}{59}.$ Now let $y$ be $C_1D.$ (thus making $C_1B = \sqrt{59} - y$ ). Similarly, we have $36 - y^2 = 25 - (\sqrt{59} - y)^2 \implies 70 = 2\sqrt{59}y \implies y = \frac{35}{\sqrt{59}} = \frac{35\sqrt{59}}{59}.$ We see that $A_1C_1$ , the scaled down diagonal is just $x - y = \frac{11\sqrt{59}}{59},$ which is $\frac{\frac{11\sqrt{59}}{59}}{\sqrt{59}} = \frac{11}{59}$ times our original diagonal $BD,$ implying a scale factor of $\frac{11}{59}.$ Thus, due to perimeters scaling linearly, the perimeter of the new quadrilateral is simply $\frac{11}{59} \cdot 22 = \frac{242}{59},$ making our answer $242+59 = \boxed{301}.$ -fidgetboss_4000

Problem 12

Solution

The expected number of steps depends on the distance between the frogs, not on the order in which these distances appear. Let $E(a,b,c)$ where $a+b+c=9$ denote the expected number of steps that it takes for two frogs to meet if traversing in clockwise or counterclockwise order, the frogs are $a$ , $b$ and $c$ vertices apart. Then $E(3,3,3)=1+\frac{1}{4} E(3,3,3)+\frac{3}{4} E(1,3,5)$ , giving $E(3,3,3)=\frac{4}{3}+E(1,3,5)$ ; (1) $E(1,3,5)=1+\frac{1}{8}E(1,1,7)+\frac{1}{2}E(1,3,5)+\frac{1}{8}E(3,3,3)$ , giving $E(1,3,5)=2+\frac{1}{4}E(1,1,7)+\frac{1}{4}E(3,3,3)$ ; (2) $E(1,1,7)=1+\frac{1}{4}E(1,1,7)+\frac{1}{4}E(1,3,5)$ , giving $E(1,1,7)=\frac{4}{3}+\frac{1}{3}E(1,3,5)$ ; (3)
Plug in (1) and (3) into (2), we see that $E(1,3,5)=4$ . $E(3,3,3)=\frac{4}{3}+4=\frac{16}{3}$ . Each step is one minute. The answer is $16+3=\boxed{19}$ .

Problem 13

Solution 1

Let $O_i$ and $r_i$ be the center and radius of $\omega_i$ , and let $O$ and $r$ be the center and radius of $\omega$ .
Since $\overline{AB}$ extends to an arc with arc $120^\circ$ , the distance from $O$ to $\overline{AB}$ is $r/2$ . Let $X=\overline{AB}\cap \overline{O_1O_2}$ . Consider $\triangle OO_1O_2$ . The line $\overline{AB}$ is perpendicular to $\overline{O_1O_2}$ and passes through $X$ . Let $H$ be the foot from $O$ to $\overline{O_1O_2}$ ; so $HX=r/2$ . We have by tangency $OO_1=r+r_1$ and $OO_2=r+r_2$ . Let $O_1O_2=d$ . $[asy] unitsize(3cm); pointpen=black; pointfontpen=fontsize(9); pair A=dir(110), B=dir(230), C=dir(310); DPA(A--B--C--A); pair H = foot(A, B, C); draw(A--H); pair X = 0.3*B + 0.7*C; pair Y = A+X-H; draw(X--1.3*Y-0.3*X); draw(A--Y, dotted); pair R1 = 1.3*X-0.3*Y; pair R2 = 0.7*X+0.3*Y; draw(R1--X); D("O",A,dir(A)); D("O_1",B,dir(B)); D("O_2",C,dir(C)); D("H",H,dir(270)); D("X",X,dir(225)); D("A",R1,dir(180)); D("B",R2,dir(180)); draw(rightanglemark(Y,X,C,3)); [/asy]$ Since $X$ is on the radical axis of $\omega_1$ and $\omega_2$ , it has equal power with respect to both circles, so $O_1X^2 - r_1^2 = O_2X^2-r_2^2 \implies O_1X-O_2X = \frac{r_1^2-r_2^2}{d}$ since $O_1X+O_2X=d$ . Now we can solve for $O_1X$ and $O_2X$ , and in particular, $\begin{align*} O_1H &= O_1X - HX = \frac{d+\frac{r_1^2-r_2^2}{d}}{2} - \frac{r}{2} \\ O_2H &= O_2X + HX = \frac{d-\frac{r_1^2-r_2^2}{d}}{2} + \frac{r}{2}. \end{align*}$ We want to solve for $d$ . By the Pythagorean Theorem (twice): $\begin{align*} &\qquad -OH^2 = O_2H^2 - (r+r_2)^2 = O_1H^2 - (r+r_1)^2 \\ &\implies \left(d+r-\tfrac{r_1^2-r_2^2}{d}\right)^2 - 4(r+r_2)^2 = \left(d-r+\tfrac{r_1^2-r_2^2}{d}\right)^2 - 4(r+r_1)^2 \\ &\implies 2dr - 2(r_1^2-r_2)^2-8rr_2-4r_2^2 = -2dr+2(r_1^2-r_2^2)-8rr_1-4r_1^2 \\ &\implies 4dr = 8rr_2-8rr_1 \\ &\implies d=2r_2-2r_1 \end{align*}$ Therefore, $d=2(r_2-r_1) = 2(961-625)=\boxed{672}$ .

Solution 2 (Official MAA, Unedited)

Denote by $O_1$ , $O_2$ , and $O$ the centers of $\omega_1$ , $\omega_2$ , and $\omega$ , respectively. Let $R_1 = 961$ and $R_2 = 625$ denote the radii of $\omega_1$ and $\omega_2$ respectively, $r$ be the radius of $\omega$ , and $\ell$ the distance from $O$ to the line $AB$ . We claim that $\dfrac{\ell}{r} = \dfrac{R_2-R_1}{d},$ where $d = O_1O_2$ . This solves the problem, for then the $\widehat{PQ} = 120^\circ$ condition implies $\tfrac{\ell}r = \cos 60^\circ = \tfrac{1}{2}$ , and then we can solve to get $d = \boxed{672}$ . $[asy] import olympiad; size(230pt); defaultpen(linewidth(0.8)+fontsize(10pt)); real r1 = 17, r2 = 27, d = 35, r = 18; pair O1 = origin, O2 = (d,0); path w1 = circle(origin,r1), w2 = circle((d,0),r2), w1p = circle(origin,r1+r), w2p = circle((d,0), r2 + r); pair[] X = intersectionpoints(w1,w2), Y = intersectionpoints(w1p,w2p); pair O = Y[1]; path w = circle(Y[1],r); pair Xp = 5 * X[1] - 4 * X[0]; pair[] P = intersectionpoints(Xp--X[0],w); label("$O_1$",origin,N); label("$O_2$",(d,0),N); label("$O$",Y[1],SW); draw(origin--Y[1]--(d,0)--cycle,gray(0.6)); pair T = foot(O,O1,O2), Tp = foot(O,X[0],X[1]); draw(Tp--O--T^^rightanglemark(O,T,O1,60)^^rightanglemark(O,Tp,X[0],60),gray(0.6)); draw(w^^w1^^w2^^P[0]--X[0]); dot(Y[1]^^origin^^(d,0)); label("$X$",T,N,gray(0.6)); label("$Y$",foot(X[0],O1,O2),NE,gray(0.6)); label("$\ell$",(O+Tp)/2,S,gray(0.6)); [/asy]$ Denote by $O_1$ and $O_2$ the centers of $\omega_1$ and $\omega_2$ respectively. Set $X$ as the projection of $O$ onto $O_1O_2$ , and denote by $Y$ the intersection of $AB$ with $O_1O_2$ . Note that $\ell = XY$ . Now recall that $d(O_2Y-O_1Y) = O_2Y^2 - O_1Y^2 = R_2^2 - R_1^2.$ Furthermore, note that $\begin{align*}d(O_2X - O_1X) &= O_2X^2 - O_1X^2= O_2O^2 - O_1O^2 \\ &= (R_2 + r)^2 - (R_1+r)^2 = (R_2^2 - R_1^2) + 2r(R_2 - R_1).\end{align*}$ Substituting the first equality into the second one and subtracting yields $2r(R_2 - R_1) = d(O_2Y - O_2X) - d(O_2X - O_1X) = 2dXY,$ which rearranges to the desired.

Solution 3 (Inversion)

WLOG assume $\omega$ is a line. Note the angle condition is equivalent to the angle between $AB$ and $\omega$ being $60^\circ$ . We claim the angle between $AB$ and $\omega$ is fixed as $\omega$ varies.
Proof: Perform an inversion at $A$ , sending $\omega_1$ and $\omega_2$ to two lines $\ell_1$ and $\ell_2$ intersecting at $B'$ . Then $\omega$ is sent to a circle tangent to lines $\ell_1$ and $\ell_2$ , which clearly intersects $AB'$ at a fixed angle. Therefore the angle between $AB$ and $\omega$ is fixed as $\omega$ varies.
Now simply take $\omega$ to be a line. If $\omega$ intersects $\omega_1$ and $\omega_2$ and $X,Y$ , respectively, and the circles' centers are $O_1$ and $O_2$ , then the projection of $O_2$ to $O_1X$ at $F$ gives that $O_2FO_1$ is a $30\text{-}60\text{-}90$ triangle. Therefore, $O_1O_2=2O_1F=2(O_1X-O_2Y)=2(961-625)=\boxed{672}.$ ~spartacle

Solution 4 (Radical Axis, Harmonic Quadrilaterals, and Similar Triangles)

Suppose we label the points as shown here. By radical axis, the tangents to $\omega$ at $D$ and $E$ intersect on $AB$ . Thus $PDQE$ is harmonic, so the tangents to $\omega$ at $P$ and $Q$ intersect at $X \in DE$ . Moreover, $OX \parallel O_1O_2$ because both $OX$ and $O_1O_2$ are perpendicular to $AB$ , and $OX = 2OP$ because $\angle POQ = 120^{\circ}$ . Thus $O_1O_2 = O_1Y - O_2Y = 2 \cdot 961 - 2\cdot 625 = \boxed{672}$

Problem 14

Solution

We first claim that $n$ must be divisible by 42. Since $\sigma(a^n)-1$ is divisible by 2021 for all positive integers $a$ , we can first consider the special case where $a \neq 0,1 \pmod{43}$ .
Then $\sigma(a^n)-1 = \sum_{i=1}^n a^i = a\left(\frac{a^n - 1}{a-1}\right)$ . In order for this expression to be divisible by $2021=43\times 47$ , a necessary condition is $a^n - 1 \equiv 0 \pmod{43}$ . By Fermat's Little Theorem, $a^{42} \equiv 1 \pmod{43}$ . Moreover, if $a$ is a primitive root modulo 43, then $\text{ord}_{43}(a) = 42$ , so $n$ must be divisible by 42.
By similar reasoning, $n$ must be divisible by 46, by considering $a \neq 0,1 \pmod{47}$ .
We next claim that $n$ must be divisible by 43 and 47. Consider the case $a=2022$ . Then $\sigma(a^n) \equiv n \pmod{2021}$ , so $\sigma(2022^n)-1$ is divisible by 2021 if and only if $n$ is divisible by 2021.
Lastly, we claim that if $n = \text{lcm}(42, 46, 43, 47)$ , then $\sigma(a^n) - 1$ is divisible by 2021 for all positive integers $a$ . The claim is trivially true for $a=1$ so suppose $a>1$ . Let $a = p_1^{e_1}\ldots p_k^{e_k}$ be the prime factorization of $a$ . Since $\sigma$ is multiplicative, we have $\sigma(a^n) - 1 = \prod_{i=1}^k \sigma(p_i^{e_in}) - 1.$ We can show that $\sigma(p_i^{e_in}) \equiv 1 \pmod{2021}$ for all primes $p_i$ and integers $e_i \ge 1$ , where $\sigma(p_i^{e_in}) = 1 + (p_i + p_i^2 + \ldots + p_i^n) + (p_i^{n+1} + \ldots + p_i^{2n}) + \ldots + (p_i^{n(e_i-1)+1} + \ldots + p_i^{e_in})$ where each expression in parentheses contains $n$ terms. It is easy to verify that if $p_i = 43$ or $p_i = 47$ then $\sigma(p_i^{e_in}) \equiv 1 \pmod{2021}$ for this choice of $n$ , so suppose $p_i \not\equiv 0 \pmod{43}$ and $p_i \not\equiv 0 \pmod{47}$ . Each expression in parentheses equals $\frac{p_i^n - 1}{p_i - 1}$ multiplied by some power of $p_i$ . If $p_i \neq 1 \pmod{43}$ , then FLT implies $p_i^n - 1 \equiv 0 \pmod{43}$ , and if $p_i \equiv 1 \pmod{43}$ , then $p_i + p_i^2 + \ldots + p_i^n \equiv 1 + 1 + \ldots + 1 \equiv 0 \pmod{43}$ (since $n$ is also a multiple of 43, by definition). Similarly, we can show $\sigma(p_i^{e_in}) \equiv 1 \pmod{47}$ , and a simple CRT argument shows $【全网首发】2021AIME I 真题及答案$ . Then $\sigma(a^n) \equiv 1^k \equiv 1 \pmod{2021}$ .
Then the prime factors of $n$ are $2$ , $3$ , $7$ , $23$ , $43$ , and $47$ , and the answer is $2+3+7+23+43+47 = \boxed{125}$ . ~scrabbler94

Solution 2 (cheap and not very reliable)

Since the problem works for all positive integers $a$ , let's plug in $a=2$ and see what we get. Since $\sigma({2^n}) = 2^{n+1}-1,$ we have $2^{n+1} \equiv 2 \pmod{2021}.$ Simplifying using CRT and Fermat's Little Theorem, we get that $2^n \equiv 0 \pmod{42}$ and $2^n \equiv 0 \pmod{46}.$ Then, we can look at $a=2022$ just like in Solution 1 to find that $43$ and $47$ also divide $n$ . There don't seem to be any other odd "numbers" to check, so we can hopefully assume that the answer is the sum of the prime factors of $\text{lcm(42, 43, 46, 47)}.$ From here, follow solution 1 to get the final answer.
-PureSwag

Solution 3 (Kind of similar to Sol 2 and kind of what cosmicgenius said)

It says the problem implies that it works for all positive integers $a$ , we basically know that If $p \equiv 1 \pmod q$ , than from "USEMO 2019 Problem 4 which was $p^n + p^{n-1} + ... + 1 \equiv 1$ (mod $q$ ) we have that $\frac{p^{en+1}-1}{p-1} \equiv p^{en} + p^{en-1} + \dots + 1 \equiv en + 1 \equiv 1 \pmod q,$ . From here we can just let $\sigma(2^n)$ or be a power of 2 which we can do $\sigma(2^n)=1+2+2^2+2^3+2^4+\cdots+2^n=2^{n+1}-1$ which is a geo series. We can plug in $a=2^a$ like in Solution 2 and use CRT which when we prime factorize we get that $2021 = 43 \cdot 47$ which like everyone knows. We use CRT to find that \begin{align*} 2^n &\equiv 1 \pmod{43}, \\ 2^n &\equiv 1 \pmod{47}. \end{align*}. We see that this is just FLT which is $a^{p-1} \equiv 1 \pmod p$ we see all multiples of 42 will work for first and 46 for the second. We can figure out that it is just $\text{lcm}(43-1,47-1)\cdot43\cdot47$ which when we add up we get that it's just the sum of the prime factors of lcm(42,43,46,47) which you can just look at Solution 1 to find out the sum of the prime factors and get the answer.
Remarks: This was kind of used in what cosmicgenius and Solution 2 said and what mathisawesome2169 said and It "Reminded me of 2019 USEMO Problem 4 when solving the $p^n + p^{n-1} + ... + 1 \equiv 1$ which gave $p \equiv 1$ $q$ . Sorry if it's bad I need to do something else so I kind of rushed.

Solution 4 (Along the line of Solution 1)

$n$ only needs to satisfy $\sigma(a^n)\equiv 1 \pmod{43}$ and $\sigma(a^n)\equiv 1 \pmod{47}$ for all $a$ . Let's work on the first requirement (mod 43) first. All $n$ works for $a=1$ . If $a>1$ , let $a$ 's prime factorization be $a=p_1^{e_1}p_2^{e_2}\cdots p_k^{e_k}$ . The following 3 statements are the same. $\text{for all }a, \sigma(a^n)=\prod_{i=1}^k(1+p_i+\cdots+p_i^{ne_i})\equiv1\pmod{43}$ $\text{for all }e>0\text{ and prime }p, 1+p+\cdots+p^{ne}\equiv1\pmod{43}$ $\text{for all prime }p, p+p^2+\cdots+p^n \equiv 0 \pmod{43}$ (1) For $p\equiv0\pmod{43}$ , no matter $n$ , it is true $p+p^2+\cdots+p^n \equiv 0 \pmod{43}$ (2) For all $p\equiv1\pmod{43}$ , $p+p^2+\cdots+p^n \equiv n \equiv 0 \pmod{43}$ One can either use brute force or Dirichlet's Theorem to show such $p$ exists. Therefore $43|n.$ (3) For all $p\not\equiv0,1\pmod{43}$ , $p+p^2+\cdots+p^n \equiv 0 \pmod{43} \Leftrightarrow p^n-1\equiv0\pmod{43}$ According to Fermat's Little Theorem, $42|n$ is sufficient. To show it's necessary we just need to show 43 has a prime primitive root. This can be done either by brute force or as follows. 43 is prime and it must have a primitive root $t$ that's coprime to 43. All numbers of the form $43k+t$ are also primitive roots of 43. According to Dirichlet's Theorem there must be primes among them.
Similar arguments for (mod 47) lead to $46|n$ and $47|n$ . Therefore $n=\text{lcm}[42,43,46,47]$

Problem 15

Solution 1

Make the translation $y \rightarrow y+20$ to obtain $20+y=x^2-k , x=2y^2-k$ . Multiply the first equation by 2 and sum, we see that $2(x^2+y^2)=3k+40+2y+x$ . Completing the square gives us $(y- \frac{1}{2})^2+(x - \frac{1}{4})^2 = \frac{325+24k}{16}$ ; this explains why the two parabolas intersect at four points that lie on a circle*. For the upper bound, observe that $LHS \leq 21^2=441 \rightarrow 24k \leq 6731$ , so $k \leq 280$ .
For the lower bound, we need to ensure there are 4 intersections to begin with. (Here I'm using the un-translated coordinates.) Draw up a graph, and realize that two intersections are guaranteed, on the so called "right branch" of $y=x^2-k$ . As we increase the value of k, two more intersections appear on the "left branch." $k=4$ does not work because the "leftmost" point of $x=2(y-20)^2-4$ is $(-4,20)$ which lies to the right of $(-\sqrt{24}, 20)$ , which is on the graph $y=x^2-4$ . While technically speaking this doesn't prove that there are no intersections (why?), drawing the graph should convince you that this is the case. Clearly, no k less than 4 works either. $k=5$ does work because the two graphs intersect at $(-5,20)$ , and by drawing the graph, you realize this is not a tangent point and there is in fact another intersection nearby, due to slope. Therefore, the answer is $5+280=285$ .

In general, (Assuming four intersections exist) when two conics intersect, if one conic can be written as $ax^2+by^2=f(x,y)$ and the other as $cx^2+dy^2=g(x,y)$ for f,g polynomials of degree at most 1, whenever $(a,b),(c,d)$ are linearly independent, we can combine the two equations and then complete the square to achieve $(x-p)^2+(y-q)^2=r^2$ . We can also combine these two equations to form a parabola, or a hyperbola, or an ellipse. When $(a,b),(c,d)$ are not L.I., the intersection points instead lie on a line, which is a circle of radius infinity. When the two conics only have 3,2 or 1 intersection points, the statement that all these points lie on a circle is trivially true.

Raybet比分 AIME课程体系流程图

Raybet比分
AIME课程体系流程图

Previous post: 斯坦福/MIT学霸都打卡的数模竞赛火热冲刺中！快来领取你的神仙队友吧~ Next post: MIT RD重磅放榜！Raybet比分有方学员霸气斩获3枚以上MIT Offers ！