- Raybet比分 提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2002AIME I真题及答案解析
2002AIME I真题及答案解析
答案解析请参考文末
Problem 1
Many states use a sequence of three letters followed by a sequence of three digits as their standard license-plate pattern. Given that each three-letter three-digit arrangement is equally likely, the probability that such a license plate will contain at least one palindrome (a three-letter arrangement or a three-digit arrangement that reads the same left-to-right as it does right-to-left) is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 2
The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as ![]() , where
, where ![]() and
and ![]() are positive integers. Find
are positive integers. Find ![]() .
.
![[asy]size(250);real x=sqrt(3); int i; draw(origin--(14,0)--(14,2+2x)--(0,2+2x)--cycle); for(i=0; i<7; i=i+1) { draw(Circle((2*i+1,1), 1)^^Circle((2*i+1,1+2x), 1)); } for(i=0; i<6; i=i+1) { draw(Circle((2*i+2,1+x), 1)); }[/asy]](https://latex.artofproblemsolving.com/2/a/d/2ad91b55f5ec02deb0493de408e8c6cd09af1421.png)
Problem 3
Jane is 25 years old. Dick is older than Jane. In ![]() years, where
years, where ![]() is a positive integer, Dick's age and Jane's age will both be two-digit number and will have the property that Jane's age is obtained by interchanging the digits of Dick's age. Let
is a positive integer, Dick's age and Jane's age will both be two-digit number and will have the property that Jane's age is obtained by interchanging the digits of Dick's age. Let ![]() be Dick's present age. How many ordered pairs of positive integers
be Dick's present age. How many ordered pairs of positive integers ![]() are possible?
are possible?
Problem 4
Consider the sequence defined by ![]() for
for ![]() . Given that
. Given that ![]() , for positive integers
, for positive integers ![]() and
and ![]() with
with ![]() , find
, find ![]() .
.
Problem 5
Let ![]() be the vertices of a regular dodecagon. How many distinct squares in the plane of the dodecagon have at least two vertices in the set
be the vertices of a regular dodecagon. How many distinct squares in the plane of the dodecagon have at least two vertices in the set ![]() ?
?
Problem 6
The solutions to the system of equations
![]() are
are ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 7
The Binomial Expansion is valid for exponents that are not integers. That is, for all real numbers ![]() ,
, ![]() , and
, and ![]() with
with ![]() ,
,
Problem 8
Find the smallest integer k for which the conditions
(1) ![]() is a nondecreasing sequence of positive integers
is a nondecreasing sequence of positive integers
(2) ![]() for all
for all ![]()
(3) ![]()
are satisfied by more than one sequence.
Problem 9
Harold, Tanya, and Ulysses paint a very long picket fence. Harold starts with the first picket and paints every ![]() th picket; Tanya starts with the second picket and paints every
th picket; Tanya starts with the second picket and paints every ![]() th picket; and Ulysses starts with the third picket and paints every
th picket; and Ulysses starts with the third picket and paints every ![]() th picket. Call the positive integer
th picket. Call the positive integer ![]()
![]() when the triple
when the triple ![]() of positive integers results in every picket being painted exactly once. Find the sum of all the paintable integers.
of positive integers results in every picket being painted exactly once. Find the sum of all the paintable integers.
Problem 10
In the diagram below, angle ![]() is a right angle. Point
is a right angle. Point ![]() is on
is on ![]() , and
, and ![]() bisects angle
bisects angle ![]() . Points
. Points ![]() and
and ![]() are on
are on ![]() and
and ![]() , respectively, so that
, respectively, so that ![]() and
and ![]() . Given that
. Given that ![]() and
and ![]() , find the integer closest to the area of quadrilateral
, find the integer closest to the area of quadrilateral ![]() .
.
![[asy]size(250); pair A=(0,12), E=(0,8), B=origin, C=(24*sqrt(2),0), D=(6*sqrt(2),0), F=A+10*dir(A--C), G=intersectionpoint(E--F, A--D); draw(A--B--C--A--D^^E--F); pair point=G+1*dir(250); label("$A$", A, dir(point--A)); label("$B$", B, dir(point--B)); label("$C$", C, dir(point--C)); label("$D$", D, dir(point--D)); label("$E$", E, dir(point--E)); label("$F$", F, dir(point--F)); label("$G$", G, dir(point--G)); markscalefactor=0.1; draw(rightanglemark(A,B,C)); label("10", A--F, dir(90)*dir(A--F)); label("27", F--C, dir(90)*dir(F--C)); label("3", (0,10), W); label("9", (0,4), W);[/asy]](https://latex.artofproblemsolving.com/1/2/0/120892a9480aa436f6a6f3c53887ace077ed8353.png)
Problem 11
Let ![]() and
and ![]() be two faces of a cube with
be two faces of a cube with ![]() . A beam of light emanates from vertex
. A beam of light emanates from vertex ![]() and reflects off face
and reflects off face ![]() at point
at point ![]() , which is
, which is ![]() units from
units from ![]() and
and ![]() units from
units from ![]() . The beam continues to be reflected off the faces of the cube. The length of the light path from the time it leaves point
. The beam continues to be reflected off the faces of the cube. The length of the light path from the time it leaves point ![]() until it next reaches a vertex of the cube is given by
until it next reaches a vertex of the cube is given by ![]() , where
, where ![]() and
and ![]() are integers and
are integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Problem 12
Let ![]() for all complex numbers
for all complex numbers ![]() , and let
, and let ![]() for all positive integers
for all positive integers ![]() . Given that
. Given that ![]() and
and ![]() , where
, where ![]() and
and ![]() are real numbers, find
are real numbers, find ![]() .
.
Problem 13
In triangle ![]() the medians
the medians ![]() and
and ![]() have lengths 18 and 27, respectively, and
have lengths 18 and 27, respectively, and ![]() . Extend
. Extend ![]() to intersect the circumcircle of
to intersect the circumcircle of ![]() at
at ![]() . The area of triangle
. The area of triangle ![]() is
is ![]() , where
, where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Problem 14
A set ![]() of distinct positive integers has the following property: for every integer
of distinct positive integers has the following property: for every integer ![]() in
in ![]() the arithmetic mean of the set of values obtained by deleting
the arithmetic mean of the set of values obtained by deleting ![]() from
from ![]() is an integer. Given that 1 belongs to
is an integer. Given that 1 belongs to ![]() and that 2002 is the largest element of
and that 2002 is the largest element of ![]() what is the greatest number of elements that
what is the greatest number of elements that ![]() can have?
can have?
Problem 15
Polyhedron ![]() has six faces. Face
has six faces. Face ![]() is a square with
is a square with ![]() face
face ![]() is a trapezoid with
is a trapezoid with ![]() parallel to
parallel to ![]()
![]() and
and ![]() and face
and face ![]() has
has ![]() The other three faces are
The other three faces are ![]() and
and ![]() The distance from
The distance from ![]() to face
to face ![]() is 12. Given that
is 12. Given that ![]() where
where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime, find
is not divisible by the square of any prime, find ![]()
2002AIME I详细解析
- Consider the three-digit arrangement,
 . There are
. There are  choices for
choices for  and
and  choices for
choices for  (since it is possible for
(since it is possible for  ), and so the probability of picking the palindrome is
), and so the probability of picking the palindrome is  . Similarly, there is a
. Similarly, there is a  probability of picking the three-letter palindrome.By the Principle of Inclusion-Exclusion, the total probability is
probability of picking the three-letter palindrome.By the Principle of Inclusion-Exclusion, the total probability is
 three digit non-palindromes, and there are
three digit non-palindromes, and there are  three letter non palindromes. As there are
three letter non palindromes. As there are  total three-letter three-digit arrangements, the probability that a license plate does not have the desired property is
total three-letter three-digit arrangements, the probability that a license plate does not have the desired property is  . We subtract this from 1 to get
. We subtract this from 1 to get  as our probability. Therefore, our answer is
as our probability. Therefore, our answer is  .
. - Let the radius of the circles be
 . The longer dimension of the rectangle can be written as
. The longer dimension of the rectangle can be written as  , and by the Pythagorean Theorem, we find that the shorter dimension is
, and by the Pythagorean Theorem, we find that the shorter dimension is  .Therefore,
.Therefore, ![$frac{14r}{2rleft(sqrt{3}+1right)}= frac{7}{sqrt{3} + 1} cdot left[frac{sqrt{3}-1}{sqrt{3}-1}right] = frac{1}{2}left(7sqrt{3} - 7right) = frac{1}{2}left(sqrt{p}-qright)$](https://latex.artofproblemsolving.com/b/a/c/bac1c28eb0b7334f0866a1e9a58d97956ee24c78.png) . Thus we have
. Thus we have  and
and  , so
, so  .Since we only care about the ratio between the longer side and shorter side, we can set the longer side to
.Since we only care about the ratio between the longer side and shorter side, we can set the longer side to  . So, this means that each of the radii is
. So, this means that each of the radii is  . Now, we connect the radii of three circles such that they form an equilateral triangle with side length 4. Obviously, the height this triangle is
. Now, we connect the radii of three circles such that they form an equilateral triangle with side length 4. Obviously, the height this triangle is  , and the shorter side if the triangle is therefore
, and the shorter side if the triangle is therefore  and we use simplification similar to as showed above, and we reach the result
and we use simplification similar to as showed above, and we reach the result  and the final answer is
and the final answer is  .
. - Let Jane's age
 years from now be
years from now be  , and let Dick's age be
, and let Dick's age be  . If
. If  , then
, then  . The possible pairs of
. The possible pairs of  are:
are:
 , so we subtract all the extraneous pairs:
, so we subtract all the extraneous pairs:  and
and  .
. 
 . Thus,
. Thus, Which means that
Which means that Since we need a factor of 29 in the denominator, we let
Since we need a factor of 29 in the denominator, we let  .* Substituting, we get
.* Substituting, we get
so

Since
 is an integer,
is an integer,  , so
, so  . It quickly follows that
. It quickly follows that  and
and  , so
, so  .
.*If
 , a similar argument to the one above implies
, a similar argument to the one above implies  and
and  , which implies
, which implies  . This is impossible since
. This is impossible since  .
.- There are 66 ways of picking two vertices. Note with any two vertices one can draw three squares (two with the vertices forming a side, another with the vertices forming the diagonal). So so far we have
 squares, but we have overcounted since some squares have their other two vertices in the dodecagon as well. All 12 combinations of two distinct vertices that form a square side only form 3 squares, and all 12 combinations of two vertices that form a square diagonal only form 6 squares. So in total, we have overcounted by
squares, but we have overcounted since some squares have their other two vertices in the dodecagon as well. All 12 combinations of two distinct vertices that form a square side only form 3 squares, and all 12 combinations of two vertices that form a square diagonal only form 6 squares. So in total, we have overcounted by  , and
, and  .
. - Let
 and let
and let  .From the first equation:
.From the first equation:  .Plugging this into the second equation yields
.Plugging this into the second equation yields  and thus,
and thus,  .So,
.So, 
 .And
.And 
 .
.
Thus,
 .
.One may simplify the work by applying Vieta's formulas to directly find that
 .
.  will always be 1, so we can ignore those terms, and using the definition (
will always be 1, so we can ignore those terms, and using the definition ( ):
):![[(10^{2002} + 1)^{frac {10}7} = 10^{2860}+dfrac{10}{7}10^{858}+dfrac{15}{49}10^{-1144}+cdots]](https://latex.artofproblemsolving.com/f/9/3/f93c3689c3938500497b7e607dd4d966f26d22dc.png) Since the exponent of the
Since the exponent of the  goes down extremely fast, it suffices to consider the first few terms. Also, the
goes down extremely fast, it suffices to consider the first few terms. Also, the  term will not affect the digits after the decimal, so we need to find the first three digits after the decimal in
term will not affect the digits after the decimal, so we need to find the first three digits after the decimal in![[dfrac{10}{7}10^{858}]](https://latex.artofproblemsolving.com/d/5/3/d5307a89b95cd1016bba711891618a1b63d7a300.png) .(The remainder after this term is positive by the Remainder Estimation Theorem). Since the repeating decimal of
.(The remainder after this term is positive by the Remainder Estimation Theorem). Since the repeating decimal of  repeats every 6 digits, we can cut out a lot of 6's from
repeats every 6 digits, we can cut out a lot of 6's from  to reduce the problem to finding the first three digits after the decimal of
to reduce the problem to finding the first three digits after the decimal of
 .
.That is the same as
 , and the first three digits after
, and the first three digits after  are
are  .
.An equivalent statement is to note that we are looking for
 , where
, where  is the fractional part of a number. By Fermat's Little Theorem,
is the fractional part of a number. By Fermat's Little Theorem,  , so
, so  ; in other words,
; in other words,  leaves a residue of
leaves a residue of  after division by
after division by  . Then the desired answer is the first three decimal places after
. Then the desired answer is the first three decimal places after  , which are
, which are  .
.- From
 ,
, 

 Suppose that
Suppose that  is the smallest possible value for
is the smallest possible value for  that yields a good sequence, and
that yields a good sequence, and  in this sequence. So,
in this sequence. So,  .Since
.Since  , the next smallest possible value for
, the next smallest possible value for  that yields a good sequence is
that yields a good sequence is  . Then,
. Then,  .By
.By  ,
,  . So the smallest value of
. So the smallest value of  is attained when
is attained when  which yields
which yields  or
or  .Thus,
.Thus,  is the smallest possible value of
is the smallest possible value of  .
. - Note that it is impossible for any of
 to be
to be  , since then each picket will have been painted one time, and then some will be painted more than once.
, since then each picket will have been painted one time, and then some will be painted more than once. cannot be
cannot be  , or that will result in painting the third picket twice. If
, or that will result in painting the third picket twice. If  , then
, then  may not equal anything not divisible by
may not equal anything not divisible by  , and the same for
, and the same for  . Now for fourth and fifth pickets to be painted,
. Now for fourth and fifth pickets to be painted,  and
and  must be
must be  as well. This configuration works, so
as well. This configuration works, so  is paintable.If
is paintable.If  is
is  , then
, then  must be even. The same for
must be even. The same for  , except that it can't be
, except that it can't be  . Thus
. Thus  is
is  and
and  is
is  . Since this is all
. Since this is all  ,
,  must be
must be  and
and  must be
must be  , in order for
, in order for  to be paint-able. Thus
to be paint-able. Thus  is paintable.
is paintable. cannot be greater than
cannot be greater than  , since if that were the case then the answer would be greater than
, since if that were the case then the answer would be greater than  , which would be impossible for the AIME.Thus the sum of all paintable numbers is
, which would be impossible for the AIME.Thus the sum of all paintable numbers is  .
.
Again, note that
 . The three conditions state that no picket number
. The three conditions state that no picket number  may satisfy any two of the conditions:
may satisfy any two of the conditions:  . By the Chinese Remainder Theorem, the greatest common divisor of any pair of the three numbers
. By the Chinese Remainder Theorem, the greatest common divisor of any pair of the three numbers  cannot be
cannot be  (since otherwise without loss of generality consider
(since otherwise without loss of generality consider  ; then there will be a common solution
; then there will be a common solution  ).
).Now for
 to be paint-able, we require either
to be paint-able, we require either  or
or  , but not both.
, but not both.- In the former condition, since
 , it follows that
, it follows that  . For
. For  and
and  to be paint-able, we require
to be paint-able, we require  , and it is easy to see that
, and it is easy to see that  works.
works. - In the latter condition, similarly we require that
 . All even numbers are painted. We now renumber the remaining odd pickets to become the set of all positive integers (
. All even numbers are painted. We now renumber the remaining odd pickets to become the set of all positive integers ( , where
, where  ), which requires the transformation
), which requires the transformation  , and with the painting starting respectively at
, and with the painting starting respectively at  . Our new number system retains the same conditions as above, except without
. Our new number system retains the same conditions as above, except without  . We thus need
. We thus need  . Then for
. Then for  to be painted, we require
to be painted, we require  . This translates to
. This translates to  , which we see works.
, which we see works.
Thus the answer is
 .
. - In the former condition, since
- By the Pythagorean Theorem,
 . Letting
. Letting  we can use the Angle Bisector Theorem on triangle
we can use the Angle Bisector Theorem on triangle  to get
to get  , and solving gives
, and solving gives  and
and  .The area of triangle
.The area of triangle  is
is  that of triangle
that of triangle  , since they share a common side and angle, so the area of triangle
, since they share a common side and angle, so the area of triangle  is
is  the area of triangle
the area of triangle  .Since the area of a triangle is
.Since the area of a triangle is  , the area of
, the area of  is
is  and the area of
and the area of  is
is  .The area of triangle
.The area of triangle  is
is  , and the area of the entire triangle
, and the area of the entire triangle  is
is  . Subtracting the areas of
. Subtracting the areas of  and
and  from
from  and finding the closest integer gives
and finding the closest integer gives  as the answer.
as the answer. - When a light beam reflects off a surface, the path is like that of a ball bouncing. Picture that, and also imagine X, Y, and Z coordinates for the cube vertices. The coordinates will all involve 0's and 12's only, so that means that the X, Y, and Z distance traveled by the light must all be divisible by 12. Since the light's Y changes by 5 and the X changes by 7 (the Z changes by 12, don't worry about that), and 5 and 7 are relatively prime to 12, the light must make 12 reflections onto the XY plane or the face parallel to the XY plane.In each reflection, the distance traveled by the light is
 =
=  . This happens 12 times, so the total distance is
. This happens 12 times, so the total distance is  .
.  and
and  , so therefore, the answer is
, so therefore, the answer is  .We can use a similar trick as with reflections in 2D: Imagine that the entire space is divided into cubes identical to the one we have. Now let's follow two photons of light that start in
.We can use a similar trick as with reflections in 2D: Imagine that the entire space is divided into cubes identical to the one we have. Now let's follow two photons of light that start in  at the same time: one of them will reflect as given in the problem statement, the second will simply fly straight through all cubes. It can easily be seen that at any moment in time the photons are in exactly the same position relative to the cubes they are inside at the moment. In other words, we can take the cube with the first photon, translate it and flip if necessary, to get the cube with the other photon.It follows that both photons will hit a vertex at the same time, and at this moment they will have travelled the same distance.Now, the path of the second photon is simply a half-line given by the vector
at the same time: one of them will reflect as given in the problem statement, the second will simply fly straight through all cubes. It can easily be seen that at any moment in time the photons are in exactly the same position relative to the cubes they are inside at the moment. In other words, we can take the cube with the first photon, translate it and flip if necessary, to get the cube with the other photon.It follows that both photons will hit a vertex at the same time, and at this moment they will have travelled the same distance.Now, the path of the second photon is simply a half-line given by the vector  . That is, the points visited by the photon are of the form
. That is, the points visited by the photon are of the form  for
for  . We are looking for the smallest
. We are looking for the smallest  such that all three coordinates are integer multiples of
such that all three coordinates are integer multiples of  (which is the length of the side of the cube).
(which is the length of the side of the cube).
Clearly
 must be an integer. As
must be an integer. As  and
and  are relatively prime, the smallest solution is
are relatively prime, the smallest solution is  . At this moment the second photon will be at the coordinates
. At this moment the second photon will be at the coordinates  .
.Then the distance it travelled is
 . And as the factorization of
. And as the factorization of  is
is  , we have
, we have  and
and  , hence
, hence  .
. - Iterating
 we get:
we get: From this, it follows that
From this, it follows that  , for all
, for all  . Thus
. Thus  Thus
Thus  .
. ![[asy] size(150); pathpen = linewidth(0.7); pointpen = black; pen f = fontsize(8); pair A=(0,0), B=(24,0), E=(A+B)/2, C=IP(CR(A,3*70^.5),CR(E,27)), D=(B+C)/2, F=IP(circumcircle(A,B,C),E--C+2*(E-C)); D(D(MP("A",A))--D(MP("B",B))--D(MP("C",C,NW))--cycle); D(circumcircle(A,B,C)); D(MP("F",F)); D(A--D); D(C--F); D(A--F--B); D(MP("E",E,NE)); D(MP("D",D,NE)); MP("12",(A+E)/2,SE,f);MP("12",(B+E)/2,f); MP("27",(C+E)/2,SW,f); MP("18",(A+D)/2,SE,f); [/asy]](https://latex.artofproblemsolving.com/2/3/6/236d2c7ecccc097482080a6f0ffbf91d00c72995.png)
 , we have:
, we have:

 .By the Power of a Point Theorem on
.By the Power of a Point Theorem on  , we get
, we get  . The Law of Cosines on
. The Law of Cosines on  gives
gives
 . Because
. Because  have the same height and equal bases, they have the same area, and
have the same height and equal bases, they have the same area, and ![$[ABF] = 2[AEF] = 2 cdot frac 12 cdot AE cdot EF sin angle AEF = 12 cdot frac{16}{3} cdot frac{sqrt{55}}{8} = 8sqrt{55}$](https://latex.artofproblemsolving.com/5/d/2/5d248af1e7003e4385df7dc89d4ce78cc9e06653.png) , and the answer is
, and the answer is  .Let
.Let  and
and  intersect at
intersect at  . Since medians split one another in a 2:1 ratio, we have
. Since medians split one another in a 2:1 ratio, we have

 and thus an easy area calculation. After extending the altitude to
and thus an easy area calculation. After extending the altitude to  and using the fact that it is also a median, we find
and using the fact that it is also a median, we find
![begin{align*} [APE] = frac{27sqrt{55}}{4} end{align*}](https://latex.artofproblemsolving.com/e/0/e/e0e0624632c79cbe43fdafe8f3101dff71656782.png)

![begin{align*} frac{[AFE]}{[APE]}=frac{[AFE]}{(frac{27sqrt{55}}{4})}=frac{EF}{PE}=frac{(frac{16}{3})}{9}=frac{16}{27} end{align*}](https://latex.artofproblemsolving.com/5/5/9/559130dec9cbc53544bcd2481dc9f3d79dc22361.png)
![begin{align*} [AFE] = 4sqrt{55} end{align*}](https://latex.artofproblemsolving.com/2/2/b/22ba94a8eb84969ae9ffeb0b51053b2b833c99de.png)
![begin{align*} [AFB]=2[AFE]=8sqrt{55} end{align*}](https://latex.artofproblemsolving.com/b/e/7/be7890f1f935bf210c7eba542b8cff2166ba0e77.png)
 .
.
Use the same diagram as in Solution 1. Call the centroid
 . It should be clear that
. It should be clear that  , and likewise
, and likewise  ,
,  . Then,
. Then,  . Power of a Point on
. Power of a Point on  gives
gives  , and the area of
, and the area of  is
is  , which is twice the area of
, which is twice the area of  or
or  (they have the same area because of equal base and height), giving
(they have the same area because of equal base and height), giving  for an answer of
for an answer of  .
.- Let the sum of the integers in
 be
be  , and let the size of
, and let the size of  be
be  . After any element
. After any element  is removed, we are given that
is removed, we are given that  , so
, so  . Since
. Since  ,
,  , and all elements are congruent to 1 mod
, and all elements are congruent to 1 mod  . Since they are positive integers, the largest element is at least
. Since they are positive integers, the largest element is at least  , the
, the  th positive integer congruent to 1 mod
th positive integer congruent to 1 mod  .We are also given that this largest member is 2002, so
.We are also given that this largest member is 2002, so  , and
, and  . Also, we have
. Also, we have  , so
, so  . The largest factor of 2001 less than 45 is 29, so
. The largest factor of 2001 less than 45 is 29, so  and
and 
 is the largest possible. This can be achieved with
is the largest possible. This can be achieved with  , for instance.
, for instance. ![[asy] size(200); import three; import graph; defaultpen(linewidth(0.7)+fontsize(8)); currentprojection=orthographic(-30,50,40); triple A=(-6,-6,0), B = (-6,6,0), C = (6,6,0), D = (6,-6,0), E = (2,0,12), H=(-6+2*sqrt(19),0,12), H1=(-6-2*sqrt(19),0,12), F, G, E1 = (6,0,12); F = 1/2*H+1/2*B; G = 1/2*H+1/2*A; draw((A--B--C--D--A)^^(D--E--C)^^(A--G--F--B)^^(G--E--F));draw((G--H--F)^^(H--E1),gray(0.6)); dot(H1^^H,linewidth(2)); label("$A$",A,( 0,-1, 0)); label("$B$",B,( 0, 1, 0)); label("$C$",C,( 0, 1, 0)); label("$D$",D,( 0,-1, 0)); label("$E$",E,(-1,-1, 1)); label("$F$",F,( 0, 1, 0)); label("$G$",G,(-1,-1, 1)); label("$H$",H,( 1,-1, 1)); label("$H'$",H1,(-1,-1, 1)); [/asy]](https://latex.artofproblemsolving.com/1/6/7/167e69f38f11e4b219976293223c73b2bdec1e72.png)
 ,
,  ,
,  and
and  . Since
. Since  is an isosceles trapezoid and
is an isosceles trapezoid and  is an isosceles triangle, we have symmetry about the
is an isosceles triangle, we have symmetry about the  -plane.Therefore, the
-plane.Therefore, the  -component of
-component of  is 0. We are given that the
is 0. We are given that the  component is 12, and it lies over the square, so we must have
component is 12, and it lies over the square, so we must have  so
so  (the other solution,
(the other solution,  does not lie over the square). Now let
does not lie over the square). Now let  and
and  , so
, so  is parallel to
is parallel to  . We must have
. We must have  , so
, so  .The last piece of information we have is that
.The last piece of information we have is that  (and its reflection,
(and its reflection,  ) are faces of the polyhedron, so they must all lie in the same plane. Since we have
) are faces of the polyhedron, so they must all lie in the same plane. Since we have  ,
,  , and
, and  , we can derive this plane.* Let
, we can derive this plane.* Let  be the extension of the intersection of the lines containing
be the extension of the intersection of the lines containing  . It follows that the projection of
. It follows that the projection of  onto the plane
onto the plane  must coincide with the
must coincide with the  , where
, where  is the projection of
is the projection of  onto the plane
onto the plane  .
.  by a ratio of
by a ratio of  , so the distance from
, so the distance from  to the plane
to the plane  is
is![[sqrt{left(sqrt{(2 times 8)^2 - 6^2}right)^2 - 12^2} = 2sqrt{19};]](https://latex.artofproblemsolving.com/1/f/1/1f10e344b2382611c9b1f040635637689f0f3305.png) and by the similarity, the distance from
and by the similarity, the distance from  to the plane
to the plane  is
is  . The altitude from
. The altitude from  to
to  has height
has height  . By similarity, the x-coordinate of
. By similarity, the x-coordinate of  is
is  . Then
. Then  .Now that we have located
.Now that we have located  , we can calculate
, we can calculate  :
:![[EG^2=(8pmsqrt{19})^2+3^2+6^2=64pm16sqrt{19}+19+9+36=128pm16sqrt{19}.]](https://latex.artofproblemsolving.com/c/2/8/c2837512e57b1f04af3d61a3c99df136c26e83ac.png) Taking the negative root because the answer form asks for it, we get
Taking the negative root because the answer form asks for it, we get  , and
, and  .
.
- One may also do this by vectors;
 , so the plane is
, so the plane is  . Since
. Since  lies on this plane, we must have
lies on this plane, we must have  , so
, so  . Therefore,
. Therefore,  . So
. So  .
.
We let
 be the origin, or
be the origin, or  ,
,  , and
, and  . Draw the perpendiculars from F and G to AB, and let their intersections be X and Y, respectively. By symmetry,
. Draw the perpendiculars from F and G to AB, and let their intersections be X and Y, respectively. By symmetry,  , so
, so  , where a and b are variables.
, where a and b are variables.We can now calculate the coordinates of E. Drawing the perpendicular from E to CD and letting the intersection be Z, we have
 and
and  . Therefore, the x coordinate of
. Therefore, the x coordinate of  is
is  , so
, so  .
.We also know that
 and
and  are coplanar, so they all lie on the plane
are coplanar, so they all lie on the plane  . Since
. Since  is on it, then
is on it, then  . Also, since
. Also, since  is contained, then
is contained, then  . Finally, since
. Finally, since  is on the plane, then
is on the plane, then  . Therefore,
. Therefore,  . Since
. Since  , then
, then  , or
, or  . Therefore, the two permissible values of
. Therefore, the two permissible values of  are
are  . The only one that satisfies the conditions of the problem is
. The only one that satisfies the conditions of the problem is  , from which the answer is
, from which the answer is  .
.- One may also do this by vectors;
以上解析方式仅供参考
学术活动报名扫码了解!免费领取历年真题!
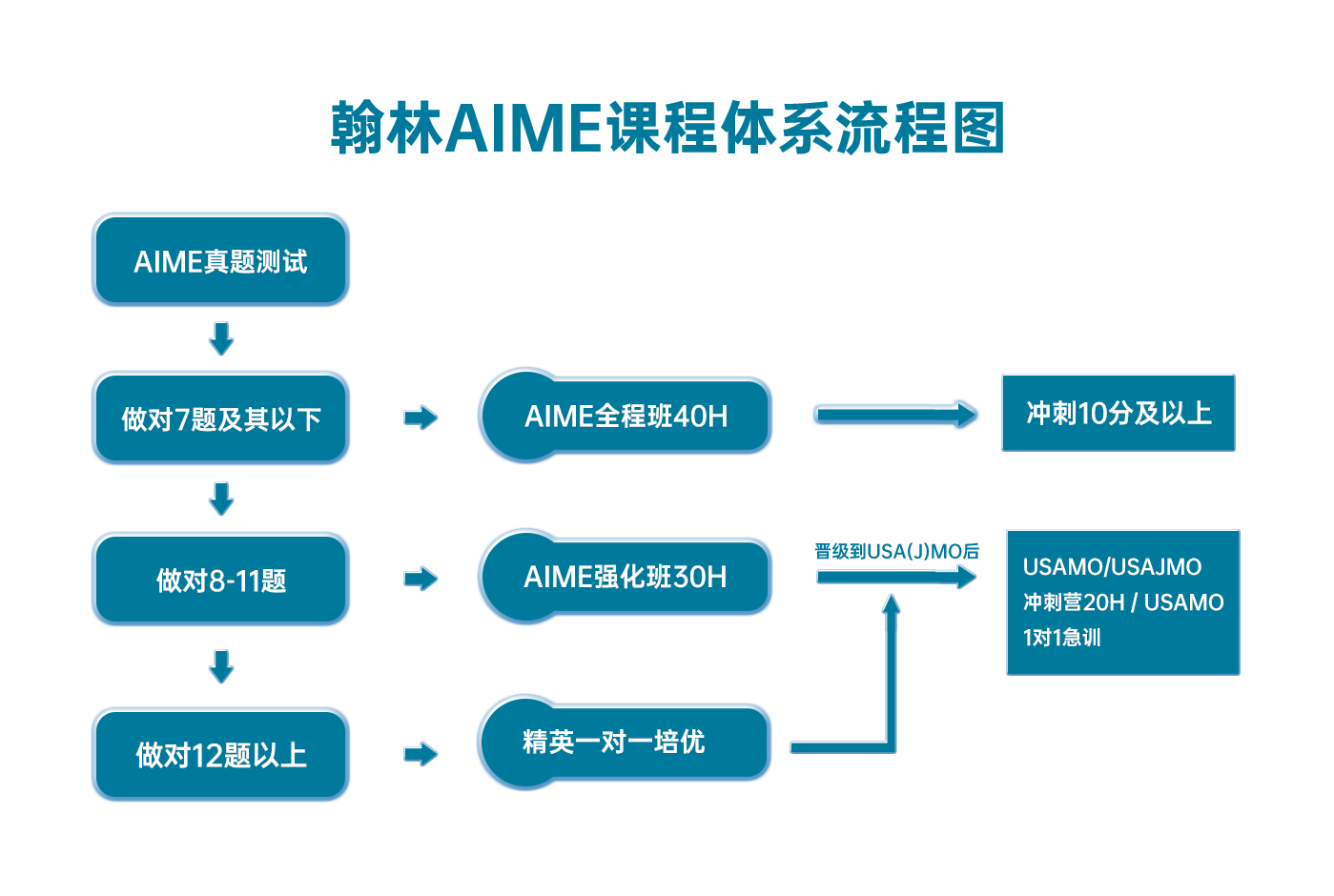
Raybet比分 AIME课程体系流程图
在线登记
最新发布
Raybet比分 课程体验,退费流程快速投诉邮箱: yuxi@linstitute.net 沪ICP备2023009024号-1